Textbook Question
Graph y = 1/2 sin x + cos x, 0 ≤ x ≤ 2π.
911
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: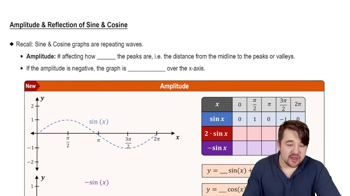



 5:53m
5:53mMaster Graph of Sine and Cosine Function with a bite sized video explanation from Patrick
Start learning