Multiple Choice
What is the exact value of ?
7
views
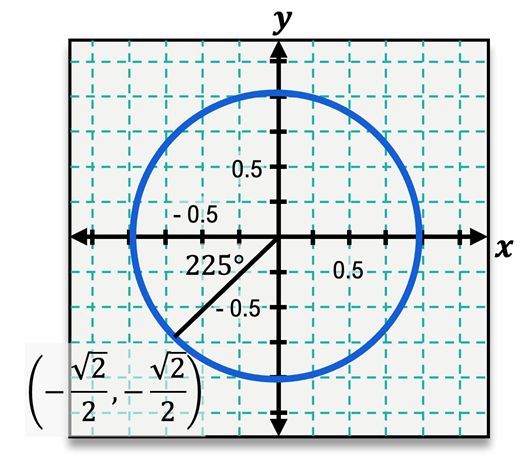
sinθ=−22,cosθ=−22,tanθ=2
sinθ=22,cosθ=−22,tanθ=−1
sinθ=−22,cosθ=−22,tanθ=1
sinθ=22,cosθ=22,tanθ=12
 Verified step by step guidance
Verified step by step guidance
 6:34m
6:34mMaster Sine, Cosine, & Tangent on the Unit Circle with a bite sized video explanation from Patrick
Start learning
