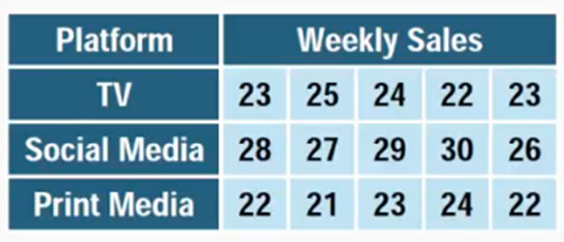
A marketing manager wants to evaluate whether three different advertising platforms-TV, social media, and print media-lead to different average sales performance across regional stores. She runs a 4-week advertising campaign, assigning one platform to a group of 5 stores each (15 stores total). After the campaign, she collects the average weekly sales (in \$1,000s) for each store during the campaign period. She wants to determine whether there is a statistically significant difference in mean sales among the three advertising platforms. State the null & alternative hypotheses for a one-way ANOVA test.

• A. $H_0$: All means are the same$H_a$: At least one advertising platform leads to a significant difference in average sales.
• B. $H_0$: At least one advertising platform leads to a significant difference in average sales. $H_{a}$: All means are the same.
• C. $H_0$: There is a significant difference in the mean sales among the three advertising platforms. $H_{a}$: There is no significant difference in the mean sales among the three advertising platforms.
• D. $H_0$: The mean sales are equal for TV advertising but differ for social media and print media platforms.$H_{a}$: The mean sales differ for all three advertising platforms.

Answer: (A)

Verified step by step guidance

1. Step 1: Define the null hypothesis (H₀) and the alternative hypothesis (Hₐ) for the one-way ANOVA test. H₀: All means are the same (no significant difference in average sales among the three advertising platforms). Hₐ: At least one advertising platform leads to a significant difference in average sales.
2. Step 2: Organize the data into groups based on the advertising platform. From the table, the weekly sales for TV are {23, 25, 24, 22, 23}, for Social Media are {28, 27, 29, 30, 26}, and for Print Media are {22, 21, 23, 24, 22}.
3. Step 3: Calculate the group means and the overall mean. The group means are the average weekly sales for each platform, and the overall mean is the average of all sales data combined.
4. Step 4: Compute the sum of squares between groups (SSB) and the sum of squares within groups (SSW). SSB measures the variation between the group means and the overall mean, while SSW measures the variation within each group.
5. Step 5: Use the ANOVA formula to calculate the F-statistic: F = (SSB / df_between) / (SSW / df_within), where df_between = number of groups - 1 and df_within = total number of observations - number of groups. Compare the F-statistic to the critical value from the F-distribution table at the chosen significance level (e.g., α = 0.05) to determine whether to reject H₀.