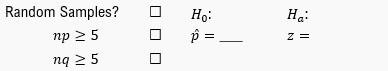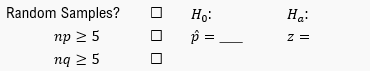Performing Hypothesis Tests: Proportions: Videos & Practice Problems

Conducting a hypothesis test for a population proportion involves four key steps: stating the null and alternative hypotheses, calculating the test statistic using the $z=\frac{\mathrm{p̂}-p}{\sqrt{p\times (1-p)/n}}$ formula, finding the p-value based on the test type (left-tailed, right-tailed, or two-tailed), and comparing the p-value to the significance level (alpha). Meeting conditions like random sampling and ensuring $np\ge 5$ and $nq\ge 5$ validates the test. This process aids in making informed decisions about population proportions using inferential statistics.

Performing Hypothesis Tests: Proportions

Hypothesis testing is a systematic method used to determine whether there is enough evidence to support a specific claim about a population parameter. In this context, we will focus on hypothesis testing for a population proportion, which involves several key steps that we will explore through a practical example.

To illustrate the process, consider a tech company that claims 90% of its devices pass inspection. A quality inspector believes the actual pass rate is lower and decides to test 200 devices, finding that 172 passed. We will conduct a hypothesis test at a significance level of 0.01 to evaluate this claim.

The first step in hypothesis testing is to formulate the hypotheses. The null hypothesis (H₀) represents the claim we are testing, which in this case is that the population proportion (p) of devices passing inspection is equal to 90%, or H₀: p = 0.9. The alternative hypothesis (H_a) reflects the inspector's belief that the pass rate is lower, expressed as H_a: p < 0.9.

Next, we calculate the test statistic using the formula for the z-score, which is given by:

z = \frac{\hat{p} - p}{\sqrt{\frac{p(1 - p)}{n}}}

Here, \(\hat{p}\) is the sample proportion, calculated as the number of successes (172) divided by the sample size (200), resulting in \(\hat{p} = 0.86\). Plugging in the values, we find:

z = \frac{0.86 - 0.9}{\sqrt{\frac{0.9(1 - 0.9)}{200}}} \approx -1.89

In the third step, we determine the p-value associated with our z-score. Since our alternative hypothesis indicates a left-tailed test, we look for the probability of obtaining a z-score less than -1.89. Using a z-table or statistical software, we find that the p-value is approximately 0.029.

Finally, we compare the p-value to our significance level (α = 0.01). Since 0.029 is greater than 0.01, we fail to reject the null hypothesis. This outcome suggests that there is insufficient evidence to conclude that the pass rate is below 90%.

Before finalizing our conclusion, we must verify that the conditions for hypothesis testing are met. First, we assume that the data was collected from a random sample unless stated otherwise. Next, we check the expected number of successes (n * p) and failures (n * q) to ensure both are at least 5. In this case:

n * p = 200 * 0.9 = 180

n * q = 200 * (1 - 0.9) = 20

Both values meet the criteria, confirming that we can draw valid conclusions from our hypothesis test.

In summary, we successfully conducted our first hypothesis test for a population proportion, demonstrating the importance of each step in the process. For further practice, consider exploring additional examples of hypothesis testing for population proportions.

Performing Hypothesis Tests: Proportions Example 1

In hypothesis testing, we begin by establishing the parameters of our study. For this scenario, we have a sample size (n) of 20, with 14 successes (x), and we are testing the claim that the population proportion (p) is 0.5 at a significance level (α) of 0.05. We will conduct three types of tests: a left-tailed test, a right-tailed test, and a two-tailed test.

Before proceeding, we must verify that the conditions for hypothesis testing are satisfied. We assume that the samples are random unless stated otherwise. Next, we check the expected number of successes and failures. The expected number of successes is calculated as \( n \cdot p = 20 \cdot 0.5 = 10 \), and the expected number of failures is \( n \cdot q = 20 \cdot (1 - 0.5) = 10 \). Both values are greater than or equal to 5, confirming that we can proceed with the tests.

We start with the left-tailed test. The null hypothesis (H₀) states that the population proportion is equal to 0.5, or \( p = 0.5 \). The alternative hypothesis (H₁) for a left-tailed test is \( p < 0.5 \). To find the sample proportion (\( \hat{p} \)), we calculate \( \hat{p} = \frac{x}{n} = \frac{14}{20} = 0.7 \). The z-score is calculated using the formula:

\( z = \frac{\hat{p} - p}{\sqrt{\frac{p(1 - p)}{n}}} = \frac{0.7 - 0.5}{\sqrt{\frac{0.5 \cdot 0.5}{20}}} \approx 1.79 \)

Using this z-score, we find the p-value, which is approximately 0.963. Since this p-value is greater than α (0.05), we fail to reject the null hypothesis, indicating insufficient evidence to support that \( p < 0.5 \).

Next, we conduct a right-tailed test. The null hypothesis remains the same, \( H₀: p = 0.5 \), while the alternative hypothesis changes to \( H₁: p > 0.5 \). The sample proportion and z-score remain unchanged, yielding \( z \approx 1.79 \). However, for the right-tailed test, we look for the area to the right of the z-score, which gives us a p-value of approximately 0.037. Since this p-value is less than α (0.05), we reject the null hypothesis, suggesting there is enough evidence to support that \( p > 0.5 \).

Finally, we perform a two-tailed test. The null hypothesis is still \( H₀: p = 0.5 \), and the alternative hypothesis is \( H₁: p \neq 0.5 \). The z-score remains at approximately 1.79. To find the p-value for a two-tailed test, we consider both tails. The area in the right tail is approximately 0.037, so we multiply this by 2, resulting in a p-value of approximately 0.073. Since this p-value is greater than α (0.05), we fail to reject the null hypothesis, indicating insufficient evidence to support that \( p \neq 0.5 \).

In summary, through these tests, we have explored the implications of our sample data on the population proportion, demonstrating how to conduct hypothesis tests and interpret the results based on p-values and significance levels.

Perform a 2-tailed hypothesis test for the true proportion of successes using the given values:
$\alpha =0.01$, $n=40$, $x=28$, & claim is $p=0.75$

• A. Because $P$-value = 0.465 > $\alpha =$ 0.01, we FAIL TO REJECT $H_0$. There is NOT ENOUGH evidence to suggest $H_a$: $p$ ≠ 0.75
• B. Because $P$-value = 0.465 > $\alpha=$ 0.01, we REJECT $H_0$. There is ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75
• C. Because $P$-value = 0.233 > $\alpha=$ 0.01, we REJECT $H_0$. There is ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75
• D. Because $P$-value = 0.233 > $\alpha=$ 0.01, we FAIL TO REJECT $H_0$. There is NOT ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75

Answer: (A)

Perform a 2-tailed hypothesis test for the true proportion of successes using the given values:
$\alpha =0.10$, $n=100$, $x=42$, & claim is $p=0.25$

• A. Because $P$-value = 0.00004 < $\alpha=$ 0.01, we FAIL TO REJECT $H_0$. There is NOT ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75
• B. Because $P$-value = 0.00004 < $\alpha=$ 0.01, we REJECT $H_0$. There is ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75
• C. Because $P$-value = 0.00008 < $\alpha=$ 0.01, we REJECT $H_0$. There is ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75
• D. Because $P$-value = 0.00008 < $\alpha=$ 0.01, we FAIL TO REJECT $H_0$. There is NOT ENOUGH evidence to suggest $H_{a}$: $p$ ≠ 0.75

Answer: (C)

Performing Hypothesis Tests: Proportions Example 2

In this scenario, we are examining whether the proportion of students participating in after-school sports at a school differs from the claimed 30%. A survey of 200 students revealed that 72 students participate in sports. To analyze this, we will conduct a hypothesis test with a significance level (alpha) of 0.01.

First, we confirm that the sample is random, which we can assume unless stated otherwise. Next, we check the conditions for the hypothesis test by calculating the expected counts. The expected number of students participating in sports, denoted as \( n \cdot p \), is calculated as follows:

\( n \cdot p = 200 \times 0.3 = 60 \)

Similarly, the expected number of students not participating in sports, denoted as \( n \cdot q \), is:

\( n \cdot q = 200 \times (1 - 0.3) = 200 \times 0.7 = 140 \)

Both expected counts (60 and 140) are greater than 5, satisfying the conditions for the test. We can now formulate our hypotheses. The null hypothesis (\( H_0 \)) states that the population proportion is equal to 0.3:

\( H_0: p = 0.3 \)

The alternative hypothesis (\( H_a \)) posits that the proportion is different from 30%:

\( H_a: p \neq 0.3 \)

This indicates that we will perform a two-tailed test. Next, we calculate the sample proportion (\( \hat{p} \)):

\( \hat{p} = \frac{x}{n} = \frac{72}{200} = 0.36 \)

Now, we compute the z-score using the formula:

\( z = \frac{\hat{p} - p}{\sqrt{\frac{p(1 - p)}{n}}} \)

Substituting the values, we have:

\( z = \frac{0.36 - 0.3}{\sqrt{\frac{0.3 \times 0.7}{200}}} \)

Calculating this gives a z-score of approximately 1.85. To find the p-value for this z-score in a two-tailed test, we look up the right tail area corresponding to the z-score and multiply it by 2. The right tail area for a z-score of 1.85 is approximately 0.032, leading to a total p-value of:

\( p \text{-value} \approx 0.064 \)

We compare this p-value to our alpha level of 0.01. Since 0.064 is greater than 0.01, we fail to reject the null hypothesis. This indicates that there is insufficient evidence to conclude that the proportion of students participating in sports is different from 30%. In summary, the analysis suggests that the school's claim about student participation in sports holds true based on the survey data.

A local park claims that less than 15% of visitors litter. A random sample of 120 visitors finds that 25 litter. At the 0.05 significance level, test if the proportion of visitors who litter is greater than 15%.

• A. Reject $H_0$, we have enough evidence to suggest p > $.15$
• B. Fail to reject $H_0$, we do NOT have enough evidence to suggest p > $.15$

Answer: (A)

Here’s what students ask on this topic:

What are the four main steps to perform a hypothesis test for a population proportion?

The four main steps to perform a hypothesis test for a population proportion are: 1) Write the hypotheses: the null hypothesis (H₀) usually states the population proportion equals a specific value, and the alternative hypothesis (H_a) states what you want to test (e.g., less than, greater than, or not equal to that value). 2) Calculate the test statistic (z-score) using the formula $z=\frac{\mathrm{p̂}-p}{\sqrt{p\divideontimes (1\; -p)/n}}$, where p̂ is the sample proportion, p is the population proportion, and n is the sample size. 3) Find the p-value corresponding to the z-score, considering the type of test (left-tailed, right-tailed, or two-tailed). 4) Compare the p-value to the significance level (α) to decide whether to reject or fail to reject the null hypothesis, and then state the conclusion in context.

How do you calculate the test statistic (z-score) in a hypothesis test for a population proportion?

To calculate the test statistic (z-score) in a hypothesis test for a population proportion, first find the sample proportion p̂ by dividing the number of successes x by the sample size n. Then use the formula: $z=\frac{\mathrm{p̂}-p}{\sqrt{p\divideontimes (1\; -p)/n}}$, where p is the hypothesized population proportion. This z-score measures how many standard deviations the sample proportion is from the hypothesized proportion, helping determine the likelihood of observing the sample data if the null hypothesis is true.

What is the role of the p-value in hypothesis testing for population proportions?

The p-value in hypothesis testing for population proportions represents the probability of obtaining a test statistic as extreme as, or more extreme than, the observed value, assuming the null hypothesis is true. It helps quantify the evidence against the null hypothesis. A small p-value (less than the significance level α) indicates strong evidence to reject the null hypothesis, suggesting the alternative hypothesis may be true. Conversely, a large p-value means there is insufficient evidence to reject the null hypothesis. The p-value is found by converting the z-score to a probability using a z-table or technology, considering the test type (left-tailed, right-tailed, or two-tailed).

How do you determine whether to reject or fail to reject the null hypothesis in a population proportion test?

To decide whether to reject or fail to reject the null hypothesis in a population proportion test, compare the p-value to the significance level α. If the p-value is less than or equal to α, reject the null hypothesis, indicating sufficient evidence to support the alternative hypothesis. If the p-value is greater than α, fail to reject the null hypothesis, meaning there is not enough evidence to support the alternative. For example, if α = 0.01 and the p-value is 0.029, since 0.029 > 0.01, we fail to reject the null hypothesis and conclude there is insufficient evidence to claim the population proportion differs from the hypothesized value.

What conditions must be met before performing a hypothesis test for a population proportion?

Before performing a hypothesis test for a population proportion, three main conditions should be met: 1) The data must come from a random sample to ensure representativeness. 2) The sample size must be large enough so that both $np$ and $nq$ (where $q=\; 1\; -p$) are at least 5. This ensures the sampling distribution of the sample proportion is approximately normal, allowing the use of the z-test. 3) The observations should be independent, which is generally true if the sample size is less than 10% of the population. Meeting these conditions validates the use of the z-test for hypothesis testing on population proportions.

How do you interpret the conclusion of a hypothesis test for a population proportion?

Interpreting the conclusion of a hypothesis test for a population proportion involves stating whether there is enough statistical evidence to support the alternative hypothesis in the context of the problem. If you reject the null hypothesis, you conclude that the sample data provide sufficient evidence that the population proportion differs from the hypothesized value in the direction specified by the alternative hypothesis. If you fail to reject the null hypothesis, you conclude that there is not enough evidence to support the alternative, meaning the population proportion is consistent with the hypothesized value. Always express the conclusion clearly and relate it back to the real-world scenario.