Linear Regression & Least Squares Method: Videos & Practice Problems

Scatter plots help visualize the correlation between two variables, with least squares regression providing a method to find the best fit line, minimizing residuals. The regression equation, typically in the form $y=ax+b$, allows for predictions within the data range. Strong correlation indicates reliable predictions, while extrapolation outside the data range should use the mean of the dependent variable instead. Understanding these concepts is crucial for effective data analysis and predictive modeling.

Intro to Least Squares Regression

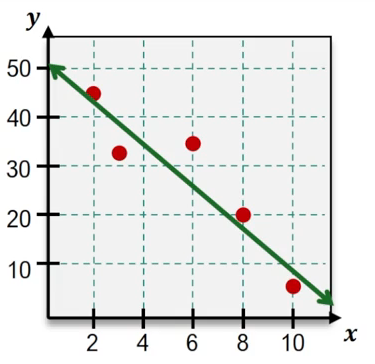
Scatter plots are a powerful tool for visualizing the relationship between two variables, typically represented as x and y values on a graph. By examining these plots, one can identify patterns and trends, such as positive or negative correlations. A positive correlation indicates that as one variable increases, the other does as well. To quantify this relationship, we can use a method known as least squares regression, which helps us find the best fit line through the data points.

Least squares regression is a statistical technique that minimizes the sum of the squares of the residuals, which are the vertical distances from each data point to the line. The goal is to find a linear equation of the form y = ax + b, where a represents the slope and b is the y-intercept. The smaller the residuals, the better the fit of the line to the data points.

To perform least squares regression using a graphing calculator, follow these steps:

1. Enable the Diagnostic On feature in your calculator to access statistical functions.
2. Input your data into the calculator, designating one list for x values and another for y values.
3. Activate the stat plot feature to visualize your data points on the graph.
4. Navigate to the stat menu, select the linear regression option, and specify the lists for x and y data. The calculator will compute the best fit line and provide the values for a and b.
5. Record the equation of the line, which will be in the form ŷ = ax + b, where ŷ denotes the predicted values.
6. Finally, input the equation into the graphing function of your calculator to visualize the best fit line alongside your data points.

For example, if you analyze ice cream sales against daily high temperatures, you might find a positive correlation where higher temperatures lead to increased sales. By applying least squares regression, you can derive a precise equation that models this relationship, allowing for predictions and deeper insights into the data.

Understanding least squares regression not only enhances your ability to interpret data but also equips you with the skills to make informed predictions based on observed trends. This method is widely applicable across various fields, including economics, biology, and social sciences, making it a valuable tool in data analysis.

The scatterplot below shows a set of data and its least-squares regression line. Based on the graph, which of the following is most likely the equation of the regression line?

• A. $\hat{y}=4.1x+50.9$
• B. $\hat{y}=-10.2x+50.9$
• C. $\hat{y}=-4.1x+50.9$
• D. $\hat{y}=-4.1x-50.9$

Answer: (C)

Intro to Least Squares Regression Example 1

In analyzing the relationship between weekly training hours and sales performance, we can utilize the least squares regression line to determine if a linear model is appropriate for the data. The process begins by entering the data into a graphing calculator, where the training hours are represented as the independent variable (x) and sales performance as the dependent variable (y).

To start, ensure that the diagnostic on feature is activated in your calculator. Next, input the x-values (1, 7, 4, 2, 6, 3, 5) into L1 and the corresponding y-values (9, 19, 25, 14, 22, 20, 23) into L2. It is crucial that both lists contain the same number of entries. After entering the data, activate the stat plot feature to visualize the scatter plot of the data points.

To compute the least squares regression line, navigate to the stat menu, select the calc tab, and choose the linReg function. Ensure that L1 is designated for x-values and L2 for y-values, then execute the calculation. The output will provide the slope (a) and y-intercept (b) of the regression line. For this dataset, the slope is approximately 1.75 and the y-intercept is about 11.86. Thus, the equation of the least squares regression line can be expressed as:

$$\hat{y} = 1.75x + 11.86$$

Next, input this equation into the y= menu of the calculator. Before graphing, adjust the window settings to ensure the data is displayed effectively. Set the x-axis range from 0 to 8 and the y-axis from 8 to 26, incrementing by 2.

Upon graphing, you will observe the plotted data points along with the regression line. However, it is important to note that the data does not fit a linear model well, as indicated by the scatter of points that do not align closely with the regression line. This suggests that the relationship between training hours and sales performance is nonlinear, which is a critical insight for further analysis.

In conclusion, while the least squares regression line provides a mathematical model, the analysis reveals that the underlying data is nonlinear, indicating that a different modeling approach may be necessary to accurately represent the relationship between the variables.

Using Regression Lines to Predict Values

In statistical analysis, particularly when working with scatter plots, one of the key applications is using regression models to predict unknown values based on known data. This process often involves the least squares method to determine the best fit regression line, which can then be utilized for making predictions.

When predicting values, two primary criteria must be met: first, there should be a strong correlation between the x and y data, indicated by an r value close to 1; second, the x value for which a prediction is being made should fall within the range of the existing data points. If both conditions are satisfied, the regression equation can be used to estimate the corresponding y value.

For example, consider a dataset that relates ice cream sales (y-axis) to temperature (x-axis). If we want to predict sales at 86 degrees Fahrenheit, we can use the regression equation derived from the data. The equation might look something like this:

ŷ = 284x - 101

By substituting 86 for x, we can calculate the predicted sales:

ŷ = 284(86) - 101 = 8323

This value indicates that at 86 degrees, the predicted ice cream sales would be 8,323 units, which aligns with the trend established by the existing data points.

However, if we attempt to predict sales at a temperature like 32 degrees Fahrenheit, which is outside the range of the dataset, the situation changes. In this case, the correlation may be weak, and extrapolating beyond the data range is not advisable. Instead, the best estimate in such scenarios is the mean of the y values, denoted as ȳ. For instance, if the mean of the y values is calculated to be 5,355, this would be the best guess for sales at 32 degrees, despite it being a less reliable estimate due to the lack of relevant data.

In summary, when using regression models for predictions, ensure that the data shows strong correlation and that the x value is within the data range. If these conditions are not met, relying on the mean of the y values is a more appropriate approach for estimation.

A regional sales manager records data on the number of clients a salesperson contacts in a week (x) and the total sales generated that week (y). The data from 10 salespeople is shown below. Find the equation of the regression line and use it to predict sales if the salesperson contacts (a) 6 clients; (b) 40 clients

• A. $\left(a\right)2,997;\left(b\right)19,147$
• B. $\left(a\right)2,997;\left(b\right)3,000$
• C. $\left(a\right)2,703;\left(b\right)18,853$
• D. $\left(a\right)2,703;\left(b\right)3,000$

Answer: (B)

Here’s what students ask on this topic:

What is the least squares regression method, and how does it work?

The least squares regression method is a statistical technique used to find the best fit line for a set of data points. It minimizes the sum of the squared residuals, where a residual is the vertical distance between a data point and the regression line. The goal is to make these residuals as small as possible, ensuring the line closely represents the data. The regression equation is typically written as $y=ax+b$, where $a$ is the slope and $b$ is the y-intercept. Calculators or software compute these values by minimizing the squared differences between observed and predicted values. This method is widely used for modeling relationships and making predictions.

How do you calculate the equation of the best fit line using a graphing calculator?

To calculate the best fit line using a graphing calculator, follow these steps: 1) Enter your data into the calculator by inputting x-values into L1 and y-values into L2. 2) Enable the 'Stat Plot' feature to visualize the scatter plot. 3) Go to the 'Stat' menu, select 'Calc,' and choose 'LinReg(ax+b).' 4) Assign L1 as the x-variable and L2 as the y-variable, then hit 'Calculate.' The calculator will output the equation in the form $y=ax+b$, where $a$ is the slope and $b$ is the y-intercept. Use this equation to plot the line or make predictions.

What is the difference between correlation and regression?

Correlation and regression are related but distinct concepts. Correlation measures the strength and direction of the linear relationship between two variables, typically represented by the correlation coefficient $r$, which ranges from -1 to 1. A value close to 1 or -1 indicates a strong relationship, while a value near 0 indicates no linear relationship. Regression, on the other hand, models the relationship between two variables by fitting an equation, such as $y=ax+b$, to the data. While correlation only describes the relationship, regression allows for predictions and quantifies how changes in one variable affect the other.

How do you use a regression line to make predictions?

To use a regression line for predictions, substitute the given x-value into the regression equation $y=ax+b$. For example, if the equation is $y=284x-16101$ and the x-value is 86, calculate $284\times 86-16101$ to find the predicted y-value. Ensure the x-value is within the data range for reliable predictions. If the x-value is outside the range, the mean of the y-values may be a better estimate, as extrapolation can lead to inaccuracies.

What are residuals, and why are they important in regression analysis?

Residuals are the differences between observed y-values and predicted y-values from a regression line. Mathematically, a residual is calculated as $e=y-ŷ$, where $y$ is the observed value and $ŷ$ is the predicted value. Residuals are important because they measure how well the regression line fits the data. In least squares regression, the line minimizes the sum of the squared residuals, ensuring the best fit. Analyzing residuals helps identify patterns, outliers, or potential issues with the model, such as non-linearity or heteroscedasticity.