Two-Way ANOVA: Videos & Practice Problems

Two-way ANOVA analyzes the effects of two factors on a dependent variable, testing for interaction effects where one factor's impact depends on the other. Hypotheses involve null and alternative statements for interaction and individual factors. The F statistic, a ratio of mean squares ($F$), and p-values determine significance at a chosen alpha ($\alpha$). Interaction plots visually assess interaction by comparing parallelism of lines, aiding interpretation of factor independence or dependence in analysis of variance (ANOVA).

Intro to Two-Way ANOVA & Two-Way Tables

Two-way ANOVA is a statistical method used to compare the means of a dependent variable across two different factors simultaneously. Unlike one-way ANOVA, which examines differences across one factor, two-way ANOVA evaluates how two independent variables influence the outcome and whether there is an interaction effect between them. For example, in studying plant growth, factors such as sunlight exposure (low, medium, high) and fertilizer level (one or three tablespoons per week) can both impact growth, and two-way ANOVA helps analyze these effects together.

In two-way ANOVA, the dependent variable is measured across all combinations of the two factors, often arranged in a data table with one factor along the rows and the other along the columns. The analysis involves testing three hypotheses: first, whether there is an interaction effect between the two factors; second, whether the first factor alone has a significant effect; and third, whether the second factor alone has a significant effect.

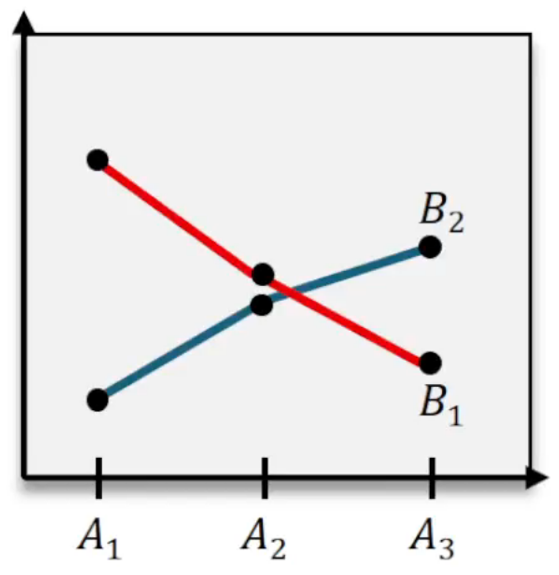
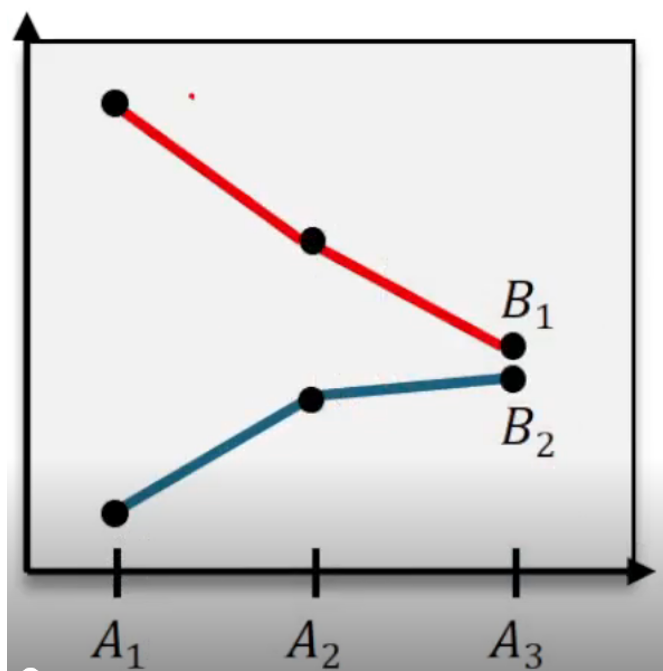
An interaction effect occurs when the effect of one factor on the dependent variable depends on the level of the other factor. For instance, if increasing fertilizer leads to a small increase in plant growth under low sunlight but a much larger increase under high sunlight, this indicates an interaction between fertilizer and sunlight. Detecting interaction is crucial because if a significant interaction exists, it complicates the interpretation of the individual effects of each factor.

The hypotheses for the interaction effect are set as follows: the null hypothesis (H₀) states that there is no interaction between the factors, while the alternative hypothesis (H₁) claims that an interaction exists. To test this, the F statistic is calculated as the ratio of the mean square due to interaction to the mean square due to error:

\[ F = \frac{\text{Mean Square Interaction}}{\text{Mean Square Error}} \]

The mean square error (MSE) represents the variability within groups and serves as the denominator in all F tests in ANOVA. If the p-value associated with the F statistic is less than the significance level (commonly α = 0.05), the null hypothesis is rejected, indicating a significant interaction effect. If the p-value is greater, the null hypothesis is not rejected, suggesting no strong evidence of interaction.

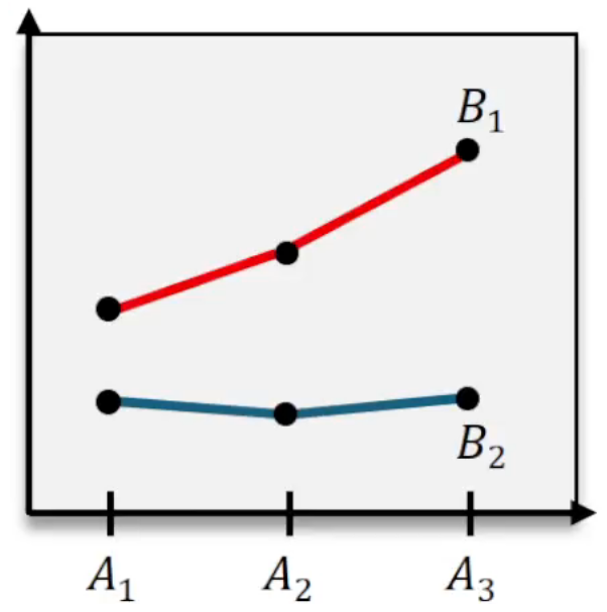
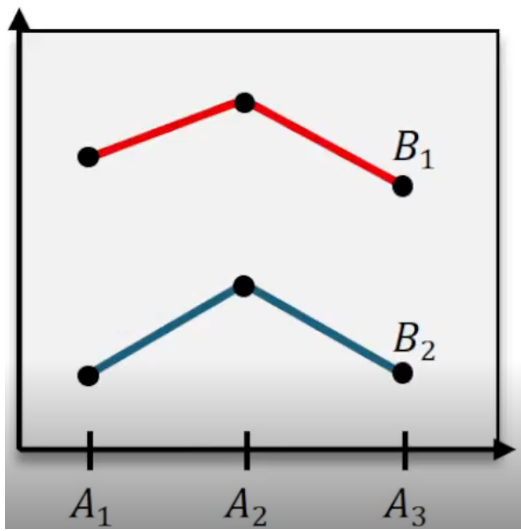
When no significant interaction is found, the analysis proceeds to test the main effects of each factor independently. Each factor's effect is tested by comparing its mean square to the mean square error, calculating an F statistic similarly:

\[ F = \frac{\text{Mean Square Factor}}{\text{Mean Square Error}} \]

For example, testing the effect of fertilizer level involves the null hypothesis that increasing fertilizer does not change plant growth, against the alternative that it does. A very small p-value (less than 0.05) leads to rejecting the null hypothesis, indicating that fertilizer level significantly affects plant growth. The same approach applies to sunlight exposure.

In summary, two-way ANOVA allows for a comprehensive analysis of how two factors and their potential interaction influence a dependent variable. The process begins by testing for interaction effects; if none are found, the main effects of each factor are evaluated separately. This method provides valuable insights into complex experimental designs where multiple factors simultaneously impact outcomes.

Which of the following scenarios can be appropriately answered using a Two-Way ANOVA test?

• A. Researchers compare final exam scores between students who attended tutoring vs. who did not
• B. A psychologist compares anxiety levels among patients receiving one of two treatments
• C. A nutritionist studies how meal type (breakfast, lunch, dinner) and diet plan (low-carb, low-fat, Mediterranean) affect blood sugar levels
• D. A professor tests if average scores on a quiz are significantly different between 5 class sections

Answer: (C)

A university surveys how study group size (solo, duo, group) and study environment (quiet, noisy) affect test performance. Which of the following conclusions most clearly suggests an interaction effect between the two factors?

• A. Students who study in quiet environments score higher than students who study in noisy ones, regardless of group size
• B. Students who study in groups generally perform better than those who study alone, regardless of environment
• C. Solo and group sizes produced similar, higher scores overall, but duo group sizes were overall lower
• D. Students studying in groups in noisy environments tend to perform better, whereas students studying solo in quiet environments tend to perform better

Answer: (D)

Intro to Two-Way ANOVA & Two-Way Tables Example 1

In analyzing a two-way ANOVA, the primary focus is to determine whether there is an interaction effect between two factors—in this case, machine type (Factor 1) and operator experience (Factor 2)—on the response variable, which is the average number of defective units produced in a month. The interaction effect examines if the influence of one factor depends on the level of the other factor. Before testing the individual main effects of machine type and operator experience, it is essential to first test for interaction because a significant interaction implies that the factors do not operate independently.

The hypotheses for the interaction effect are set as follows: the null hypothesis assumes no interaction between the factors, while the alternative hypothesis suggests that an interaction exists. To test this, the p-value associated with the interaction term in the ANOVA table is compared to the significance level, typically α = 0.05. If the p-value is less than α, the null hypothesis is rejected, indicating evidence of interaction.

For example, if the p-value for the interaction effect is 0.027, which is less than 0.05, this leads to rejecting the null hypothesis and concluding that there is a statistically significant interaction between machine type and operator experience. This means the effect of machine type on defective units depends on the operator’s experience level, or vice versa.

When a significant interaction is found, it is generally inappropriate to interpret the main effects independently because the factors influence each other. However, if required, the main effects can still be examined with caution. For the main effects, the p-values are compared to the same significance level. For instance, a p-value of 0.052 for machine type is slightly above 0.05, leading to a failure to reject the null hypothesis, indicating no significant main effect of machine type alone. Similarly, a p-value of 0.556 for operator experience also results in failing to reject the null hypothesis, showing no significant main effect for operator experience independently.

In summary, the presence of a significant interaction effect in a two-way ANOVA suggests that the combined influence of machine type and operator experience affects the number of defective units produced, and this interaction should be the focus of interpretation. The main effects should be interpreted cautiously or not at all if the interaction is significant, as the factors do not act independently in influencing the response variable.

Two-Way ANOVA: Interaction Plots

In analyzing the effects of two factors on a dependent variable, an interaction plot provides a visual method to detect interaction effects between factors. Interaction effects occur when the influence of one factor on the response variable depends on the level of the other factor. For example, consider a study examining how hours of sleep (factor one) and study time (factor two) affect student performance on a nationwide exam. The exam scores serve as the dependent variable, plotted on the y-axis, while one factor, such as hours of sleep, is placed on the x-axis.

To construct an interaction plot, the levels of the second factor (e.g., low and high study time) are represented by separate lines on the graph. Each line connects the mean exam scores corresponding to the different levels of the x-axis factor. For instance, plotting exam scores at 4, 6, and 8 hours of sleep for both low and high study time creates two distinct lines. These lines are then analyzed to determine if they are parallel or not.

The key to interpreting interaction plots lies in the slopes of these lines. If the lines are approximately parallel, it suggests no interaction effect, meaning the effect of one factor on exam scores is consistent regardless of the other factor’s level. Conversely, if the lines diverge, cross, or have different slopes, this indicates an interaction effect, where the impact of one factor varies depending on the other. For example, if students who sleep more show a greater increase in exam scores with increased study time compared to those who sleep less, the lines will not be parallel, signaling an interaction.

While interaction plots provide a straightforward, visual approach to identifying potential interaction effects, statistical tests such as two-way ANOVA are necessary to confirm these findings rigorously. Nonetheless, understanding how to create and interpret interaction plots is essential for exploring complex relationships between multiple factors in experimental data.

In summary, interaction plots graphically display the relationship between two factors and a dependent variable, with the presence of non-parallel lines indicating interaction effects. This method enhances comprehension of how combined factors influence outcomes, a critical concept in experimental design and data analysis.

Which of the following interaction plots best indicates no interaction between the two factors?

• A.
• B.
• C.
• D.

Answer: (C)

Here’s what students ask on this topic:

What is the main purpose of conducting a two-way ANOVA?

Two-way ANOVA is used to analyze the effects of two different factors on a dependent variable simultaneously. It helps determine not only the individual impact of each factor but also whether there is an interaction effect between the two factors. An interaction effect occurs when the effect of one factor depends on the level of the other factor. This method extends the one-way ANOVA by allowing comparison across two factors, making it useful for more complex experimental designs where multiple variables influence the outcome.

How do you interpret interaction effects in a two-way ANOVA?

Interaction effects in two-way ANOVA indicate that the effect of one factor on the dependent variable changes depending on the level of the other factor. To interpret this, you first test the null hypothesis that there is no interaction. If the p-value for the interaction term is less than the significance level (usually 0.05), you reject the null hypothesis, concluding that an interaction exists. This means the factors do not act independently, and the effect of one factor varies with the other. If the p-value is greater, you fail to reject the null, suggesting no significant interaction.

What is an interaction plot and how is it used in two-way ANOVA?

An interaction plot is a graphical tool used to visually assess interaction effects between two factors in a two-way ANOVA. It plots the dependent variable on the y-axis and one factor on the x-axis, with separate lines representing levels of the second factor. If the lines are roughly parallel, it suggests no interaction effect, meaning the factors act independently. If the lines cross or diverge, it indicates a potential interaction effect, where the influence of one factor depends on the other. This plot helps in understanding the relationship before conducting formal statistical tests.

How are F statistics calculated in a two-way ANOVA?

In two-way ANOVA, F statistics are calculated as ratios of mean squares (MS). For each factor and the interaction, the F statistic is computed by dividing the mean square of that factor or interaction by the mean square error (MSE). Mathematically, for a factor A, the F statistic is $\frac{\mathrm{MS\_A}}{\mathrm{MS\_E}}$, where $\mathrm{MS\_A}$ is the mean square for factor A and $\mathrm{MS\_E}$ is the mean square error. This ratio tests whether the variance explained by the factor is significantly greater than the unexplained variance, helping determine if the factor has a significant effect on the dependent variable.

What are the null and alternative hypotheses in a two-way ANOVA?

In two-way ANOVA, there are three sets of hypotheses: one for each factor and one for the interaction. For each factor, the null hypothesis ($\mathrm{H\_0}$) states that there is no difference in means across the levels of that factor, while the alternative hypothesis ($\mathrm{H\_a}$) states that at least one mean is different. For the interaction, the null hypothesis states that there is no interaction effect between the two factors, meaning their effects are independent. The alternative hypothesis states that there is an interaction effect, meaning the effect of one factor depends on the level of the other.