Given the triangle below, determine the missing side(s) without using the Pythagorean theorem (make sure your answer is fully simplified).

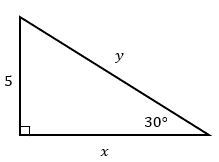
• A. $x=10,y=5\sqrt5$
• B. $x=3,y=4$
• C. $x=5\sqrt3,y=10$
• D. $x=5,y=5\sqrt2$

Answer: (C)

Verified step by step guidance

1. Identify the type of triangle: The given triangle is a right triangle with one angle measuring 30 degrees.
2. Recall the properties of a 30-60-90 triangle: In such a triangle, the side opposite the 30-degree angle is half the hypotenuse, and the side opposite the 60-degree angle is the square root of 3 times the shorter leg.
3. Given that the side opposite the 30-degree angle is 5, set the hypotenuse y to be twice this length, i.e., y = 2 * 5.
4. Calculate the length of the side x, which is opposite the 60-degree angle, using the property: x = 5 * sqrt(3).
5. Verify the solution by checking that the calculated sides satisfy the properties of a 30-60-90 triangle.