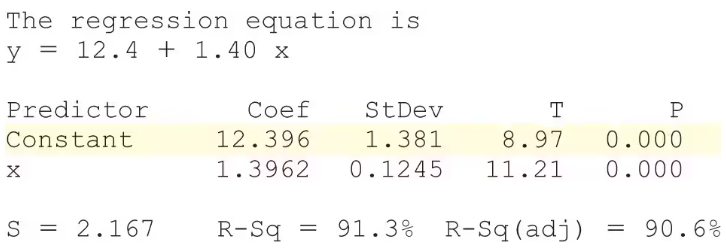
In Problems 5–10, use the results of Problems 7–12, respectively, from Section 4.2 to answer the following questions:
a. What are the estimates of β₀ and β₁?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 7:01m
7:01mMaster Intro to Least Squares Regression with a bite sized video explanation from Patrick
Start learning