When can the Empirical Rule be used to identify unusual results in a binomial experiment? Why can the Empirical Rule be used to identify results in a binomial experiment?

Verified step by step guidance

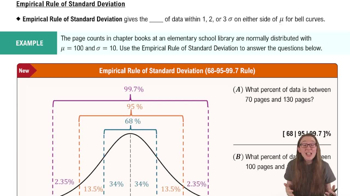
1. Step 1: Understand the Empirical Rule, which states that for a normal distribution, approximately 68% of data falls within 1 standard deviation of the mean, 95% within 2 standard deviations, and 99.7% within 3 standard deviations.
2. Step 2: Recognize that the Empirical Rule applies directly to normal distributions, so to use it for a binomial experiment, the binomial distribution must be approximately normal.
3. Step 3: Identify the conditions under which a binomial distribution can be approximated by a normal distribution: when both \(n p \geq 10\) and \(n (1 - p) \geq 10\), where \(n\) is the number of trials and \(p\) is the probability of success.
4. Step 4: Calculate the mean \(\mu = n p\) and the standard deviation \(\sigma = \sqrt{n p (1 - p)}\) of the binomial distribution to apply the Empirical Rule.
5. Step 5: Use the Empirical Rule to determine if a result is unusual by checking if it lies more than 2 or 3 standard deviations away from the mean, indicating it is unlikely under the binomial model.

Key Concepts

Empirical Rule

The Empirical Rule states that for a normal distribution, about 68% of data falls within one standard deviation, 95% within two, and 99.7% within three. It helps identify unusual results by showing how far a value deviates from the mean in terms of standard deviations.

Binomial Distribution Approximation to Normal

A binomial distribution can be approximated by a normal distribution when the number of trials is large and both np and n(1-p) are greater than 5. This allows the use of normal-based methods, like the Empirical Rule, to analyze binomial outcomes.

Identifying Unusual Results

Unusual results in a binomial experiment are outcomes that lie far from the expected value, typically beyond two or three standard deviations. Using the Empirical Rule on the normal approximation helps determine if a result is statistically rare or unusual.