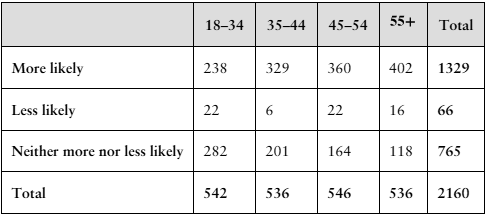
Multiple Choice
Which sampling method involves dividing the population into groups () and then taking a random sample from each group?
22
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 5:37m
5:37mMaster Introduction to Probability with a bite sized video explanation from Patrick
Start learning