The green dotted line in the graph below represents the function f(x)f\left(x\right)f(x). The blue solid line represents the function g(x)g\left(x\right)g(x), which is the function f(x)f\left(x\right)f(x)after it has gone through a shift transformation. Find the equation for g(x)g\left(x\right)g(x).

g ( x ) = f ( x + 2 ) − 3 g\left(x\right)=f\left(x+2\right)-3 g ( x ) = f ( x + 2 ) − 3

The green dotted line in the graph below represents the function f ( x ) f\left(x\right) f ( x ) . The blue solid line represents the function g ( x ) g\left(x\right) g ( x ) , which is the function f ( x ) f\left(x\right) f ( x ) after it has gone through a shift transformation. Find the equation for g ( x ) g\left(x\right) g ( x ) .

Alright. So let's give this problem a try. So here we have that the green dotted line in the graph below represents the function f of x, and that's gonna be this curve that we see right here. Now we're told that the blue solid line represents the function g of x, which is the function f of x after it has gone through a shift transformation. We're asked to find the equation for g of x. Now recall that when a function goes through a shift, you start with your original function f of x, and this becomes f of x minus h plus k. This was the general form for a shift that we discussed in our videos on the shift transformation. Now we can see here that our original function started here at the center, 0, and what happened is this graph got shifted to this position. Well, we can see here that it got shifted down 1, 2, 3 units, and we can see here that it got shifted left 1, 2 units. So what we could do here and I said 2 units because it went 2 positions over from the origin. So what we can do is say that the h value which represents the horizontal shift is negative 2, so it shifted left 2 units, and we can say that the k value, which represents the vertical shift, shifted down 3 units, so it's negative 3. So what our function is going to end up looking like is g of x is going to be f of x minus h plus k, where we have f of x minus, and then our h value is negative 2. So we have f of x minus negative 2, plus the k value, which we said here was negative 3. So this is what our shift is going to look like, but we can clean this up algebraically a bit, because we can cancel this negative sign right here, these two negative signs. So So what this is really going to end up end up being is that g of x is equal to f of x plus 2, and then this is going to be minus 3. So we can just write this as minus 3 since plus negative 3 is the same thing as minus 3. So g of x is going to end up looking like this, and this will be our transform function as an equation. So that is how you can solve this problem. Let's move on.

The green dotted line in the graph below represents the function f ( x ) f\left(x\right) f ( x ) . The blue solid line represents the function g ( x ) g\left(x\right) g ( x ) , which is the function f ( x ) f\left(x\right) f ( x ) after it has gone through a shift transformation. Find the equation for g ( x ) g\left(x\right) g ( x ) .

g ( x ) = f ( x + 2 ) − 3 g\left(x\right)=f\left(x+2\right)-3 g ( x ) = f ( x + 2 ) − 3

g ( x ) = f ( x − 2 ) + 3 g\left(x\right)=f\left(x-2\right)+3 g ( x ) = f ( x − 2 ) + 3

g ( x ) = f ( x − 2 ) − 3 g\left(x\right)=f\left(x-2\right)-3 g ( x ) = f ( x − 2 ) − 3

g ( x ) = f ( x ) − 3 g\left(x\right)=f\left(x\right)-3 g ( x ) = f ( x ) − 3

0. Review of College Algebra

Transformations

Trigonometry

0. Review of College Algebra

Transformations

Struggling with Trigonometry?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

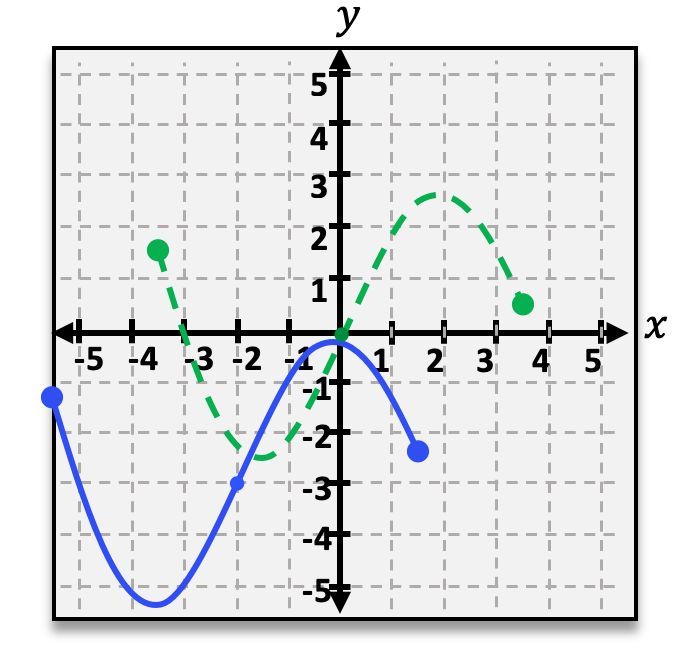
The green dotted line in the graph below represents the function $f\left(x\right)$ . The blue solid line represents the function $g\left(x\right)$ , which is the function $f\left(x\right)$ after it has gone through a shift transformation. Find the equation for $g\left(x\right)$ .

$g\left(x\right)=f\left(x-2\right)+3$

$g\left(x\right)=f\left(x-2\right)-3$

$g\left(x\right)=f\left(x+2\right)-3$

$g\left(x\right)=f\left(x\right)-3$

Verified step by step guidance

Identify the transformation from the graph: The green dotted line is the original function f(x), and the blue solid line is the transformed function g(x).

Observe the horizontal shift: The green function f(x) is shifted to the left to become the blue function g(x). This indicates a horizontal shift to the left by 2 units.

Observe the vertical shift: The green function f(x) is shifted downwards to become the blue function g(x). This indicates a vertical shift down by 3 units.

Combine the transformations: A horizontal shift to the left by 2 units is represented by f(x + 2), and a vertical shift down by 3 units is represented by subtracting 3.

Write the equation for g(x): Combine the horizontal and vertical shifts to get g(x) = f(x + 2) - 3.

5:25m

Watch next

Master Introduction to Transformations with a bite sized video explanation from Patrick

Start learning

Transformations practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice