Written below (green dotted curve) is a graph of the function f(x)=x−2f\left(x\right)=\sqrt{x-2}f(x)=x−2.If g(x) (blue solid curve) is a reflection of f(x) about the y-axis what is the equation for g(x)?

g ( x ) = − x − 2 g\left(x\right)=\sqrt{-x-2} g ( x ) = − x − 2 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z">

Written below (green dotted curve) is a graph of the function f ( x ) = x − 2 f\left(x\right)=\sqrt{x-2} f ( x ) = x − 2 <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429c69,-144,104.5,-217.7,106.5,-221l0 -0c5.3,-9.3,12,-14,20,-14H400000v40H845.2724s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47zM834 80h400000v40h-400000z"> .If g(x) (blue solid curve) is a reflection of f(x) about the y-axis what is the equation for g(x) ?

Okay. Let's give this problem a try. So here we have that written below is the function f of x is equal to the square root of x minus 2. We also have g of x, which is a function graphed on here as well, and we're asked if g of x is a reflection of f of x about the y axis, what is the equation for g of x? Now whenever you see that something is reflected about the y axis, this is the same thing as saying it's reflected over the y axis. So in the same sense that we've been learning about reflections, it's like we took this this entire graph, increased it at the y, and we folded it over. Now this was our original function f of x, which is this green dotted line, and we're asked what the equation is going to be for our reflected function g of x. Now to figure this out, recall that we have a situation where we're we reflect over the y, and when this happens, your original function f of x is going to become f of negative x, and the reason for this is because it's the signs of the x values that change. You'll notice if you look at one x value here we start at positive 3 right there, and then we finish at negative 3. It's the same y value that we have at on the y axis, but it changes to negative the negative x values, so that is why we say it's the inside of the function that changes. We discussed this in the video on reflections. So let's see what this new equation is going to look like. If our original function is that f of x is equal to the square root of x minus 2, like we see up here, then our transform function g of x is going to be the negative version of this. So it's gonna be f of negative x, and f of negative x is just going to be a negative sign on this x here, so it'll be negative x minus 2 or the square root of negative x minus 2, I should say. So this right here would be our transformed function, g of x, and that is how you can solve these types of problems. Hope you found this helpful. Let me know if you have any questions.

Written below (green dotted curve) is a graph of the function f ( x ) = x − 2 f\left(x\right)=\sqrt{x-2} f ( x ) = x − 2 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z"> . If g(x) (blue solid curve) is a reflection of f(x) about the y-axis what is the equation for g(x) ?

g ( x ) = − x − 2 g\left(x\right)=\sqrt{-x-2} g ( x ) = − x − 2 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z">

g ( x ) = − x − 2 g\left(x\right)=\sqrt{-x}-2 g ( x ) = − x <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z"> − 2

g ( x ) = x − 2 g\left(x\right)=\sqrt{x-2} g ( x ) = x − 2 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z">

g ( x ) = x − 2 g\left(x\right)=\sqrt{x}-2 g ( x ) = x <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z"> − 2

0. Review of College Algebra

Transformations

Trigonometry

0. Review of College Algebra

Transformations

Struggling with Trigonometry?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Written below (green dotted curve) is a graph of the function $f\left(x\right)=\sqrt{x-2}$ .If g(x) (blue solid curve) is a reflection of f(x) about the y-axis what is the equation for g(x)?

$g\left(x\right)=\sqrt{-x-2}$

$g\left(x\right)=\sqrt{-x}-2$

$g\left(x\right)=\sqrt{x-2}$

$g\left(x\right)=\sqrt{x}-2$

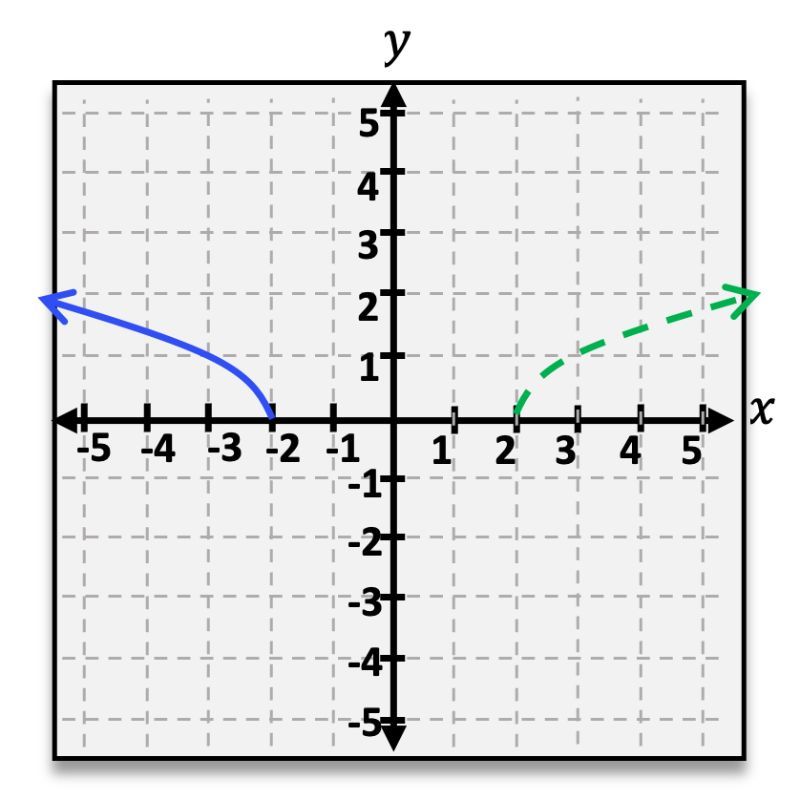
Verified step by step guidance

Identify the given function f(x) = \sqrt{x - 2}. This function is defined for x >= 2, and its graph is the green dotted curve.

Understand that reflecting a function about the y-axis involves replacing x with -x in the function's equation.

Apply the reflection transformation to f(x): replace x with -x in the equation f(x) = \sqrt{x - 2} to get g(x) = \sqrt{-x - 2}.

Note that the domain of g(x) = \sqrt{-x - 2} is x <= -2, which matches the blue solid curve on the graph.

Conclude that the equation for g(x), the reflection of f(x) about the y-axis, is g(x) = \sqrt{-x - 2}.

5:25m

Watch next

Master Introduction to Transformations with a bite sized video explanation from Patrick

Start learning

Transformations practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice