Use each graph to obtain the graph of the corresponding reciprocal function, cosecant or secant. Give the equation of the function for the graph that you obtain.
<IMAGE>
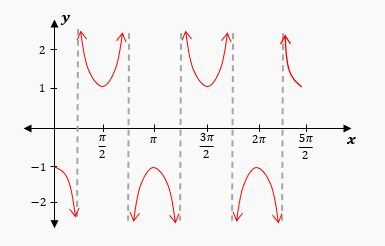
b=2
b=4
b=2π
b=π
 Verified step by step guidance
Verified step by step guidance
 6:22m
6:22mMaster Graphs of Secant and Cosecant Functions with a bite sized video explanation from Patrick
Start learning
