Triangles are fundamental geometric shapes characterized by three sides that close to form a shape. Understanding the different types of triangles based on their side lengths and angles is essential for further studies in geometry.
Triangles can be classified into three categories based on the lengths of their sides:
- Equilateral Triangle: All three sides are of equal length. For example, if each side measures 3 units, it is an equilateral triangle. This is indicated in diagrams by tick marks next to the side lengths.
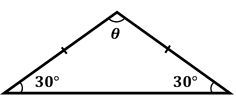
- Isosceles Triangle: Two sides are of equal length, while the third side is different. For instance, if two sides measure 5 units and the base measures 3 units, it is an isosceles triangle.
- Scalene Triangle: All sides have different lengths. An example would be sides measuring 3, 5, and 6 units.
In addition to side lengths, triangles can also be classified based on their angles:
- Acute Triangle: All angles are less than 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees. For example, if two angles measure 35 degrees and one measures 110 degrees, it is an obtuse triangle.
- Right Triangle: One angle is exactly 90 degrees, which is a key focus in many geometric applications.
A crucial property of triangles is that the sum of all interior angles always equals 180 degrees. This fundamental rule allows for the calculation of missing angles. For instance, if two angles in a triangle measure 40 degrees each, the third angle can be found by setting up the equation:
\[40 + 40 + \theta = 180\]By solving for \(\theta\), we find that \(\theta = 100\) degrees, indicating that the triangle is obtuse.
Understanding these classifications and properties of triangles lays a solid foundation for more complex geometric concepts and problem-solving techniques. As you practice, remember to apply these principles to identify triangle types and calculate missing angles or sides effectively.