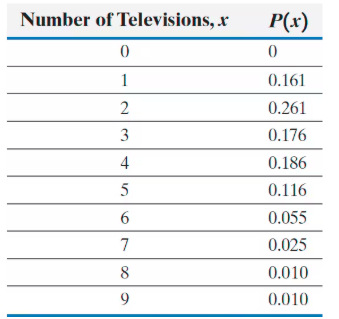
[NW] [DATA] TelevisionsIn the Sullivan Statistics Survey I, individuals were asked to disclose the number of televisions in their household. In the following probability distribution, the random variable X represents the number of televisions in households.
a. Confirm that this represents a discrete probability distribution.

Verified step by step guidance

1. Step 1: Verify that the random variable X is discrete by checking if it takes on countable values. Here, X represents the number of televisions, which are whole numbers from 0 to 9, so X is discrete.
2. Step 2: Check that each probability value P(x) is between 0 and 1 inclusive. Review the given probabilities: 0, 0.161, 0.261, 0.176, 0.186, 0.116, 0.055, 0.025, 0.010, and 0.010. All these values satisfy 0 \leq P(x) \leq 1.
3. Step 3: Confirm that the sum of all probabilities equals 1. Calculate the sum using the formula: \(\sum_{x=0}^{9} P(x) = 0 + 0.161 + 0.261 + 0.176 + 0.186 + 0.116 + 0.055 + 0.025 + 0.010 + 0.010\).
4. Step 4: If the sum from Step 3 equals 1, then the set of probabilities forms a valid probability distribution for the discrete random variable X.
5. Step 5: Conclude that since X is discrete, all probabilities are between 0 and 1, and their sum is 1, this table represents a discrete probability distribution.

Key Concepts

Discrete Probability Distribution

A discrete probability distribution lists all possible values of a discrete random variable and their associated probabilities. Each probability must be between 0 and 1, and the sum of all probabilities must equal 1. This ensures the distribution accurately represents the likelihood of each outcome.

Random Variable

A random variable is a numerical outcome of a random phenomenon. In this case, X represents the number of televisions in a household, which can only take integer values. Understanding the random variable helps in interpreting the probability distribution and analyzing the data.

Probability Sum Rule

The probability sum rule states that the total probability of all possible outcomes must be exactly 1. This rule is essential to confirm that a given set of probabilities forms a valid probability distribution, ensuring that all possible events are accounted for.