Multiple Choice
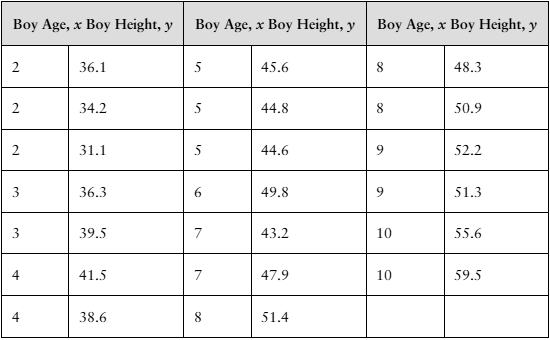
In residuals analysis, what should the residual plot look like if the regression line fits the data well?
42
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 7:38m
7:38mMaster Residuals and Residual Plots with a bite sized video explanation from Patrick
Start learning