Testing the Difference Between Two Means (c) calculate d̄ and Sd, Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)

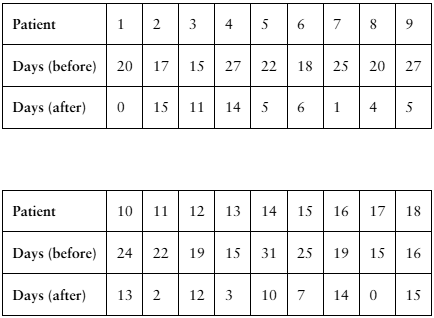
Verified step by step guidance

1. Step 1: Calculate the differences (d) for each patient by subtracting the 'Days after' value from the 'Days before' value. For example, for Patient 1, d = 20 - 0 = 20.
2. Step 2: Compute the mean of the differences (d̄) by summing all the differences and dividing by the total number of patients. Use the formula: $\mathrm{d̄}=\frac{\sum d}{n}$, where n is the number of patients.
3. Step 3: Calculate the standard deviation of the differences (Sd) using the formula: $Sd=\sqrt{\frac{\sum (d-\mathrm{d̄}{)}^2}{n-1}}$, where d̄ is the mean difference and n is the number of patients.
4. Step 4: Perform a t-test for dependent samples to test the null hypothesis that the mean difference is zero. Use the formula for the t-statistic: $t=\frac{\mathrm{d̄}}{\frac{S}{d}/\sqrt{n}}$, where Sd is the standard deviation of the differences and n is the number of patients.
5. Step 5: Compare the calculated t-statistic to the critical t-value at α = 0.01 and degrees of freedom (df = n - 1). If the calculated t-statistic exceeds the critical t-value, reject the null hypothesis and conclude that there is enough evidence to support the researcher's claim.

Key Concepts

Dependent Samples

Dependent samples, also known as paired samples, occur when the same subjects are measured under different conditions or at different times. In this context, the number of migraine days before and after treatment for the same patients is compared. This design helps control for individual variability, allowing for a more accurate assessment of the treatment's effect.

Mean Difference (d̄)

The mean difference (d̄) is calculated by finding the average of the differences between paired observations. In this case, it represents the average change in the number of migraine days for patients before and after receiving the treatment. This statistic is crucial for determining whether the treatment has a significant effect on reducing migraine days.

Standard Deviation of Differences (Sd)

The standard deviation of differences (Sd) measures the variability of the differences between paired observations. It provides insight into how consistent the treatment effect is across patients. A smaller Sd indicates that the treatment has a more uniform effect, while a larger Sd suggests greater variability in responses, which is important for hypothesis testing.