Understanding the concepts of relations and functions is essential in mathematics, particularly when analyzing graphs. A relation is defined as a connection between sets of values, specifically X (input) and Y (output) values, which can be represented graphically as ordered pairs. In contrast, a function is a specific type of relation where each input corresponds to at most one output. This distinction is crucial: while all functions are relations, not all relations qualify as functions.
To determine whether a relation is a function, one can analyze the inputs and outputs. For instance, if a particular input has multiple outputs, the relation cannot be classified as a function. This can be illustrated through examples where the X values are listed alongside their corresponding Y values. If any X value is associated with more than one Y value, the relation fails the function criteria.
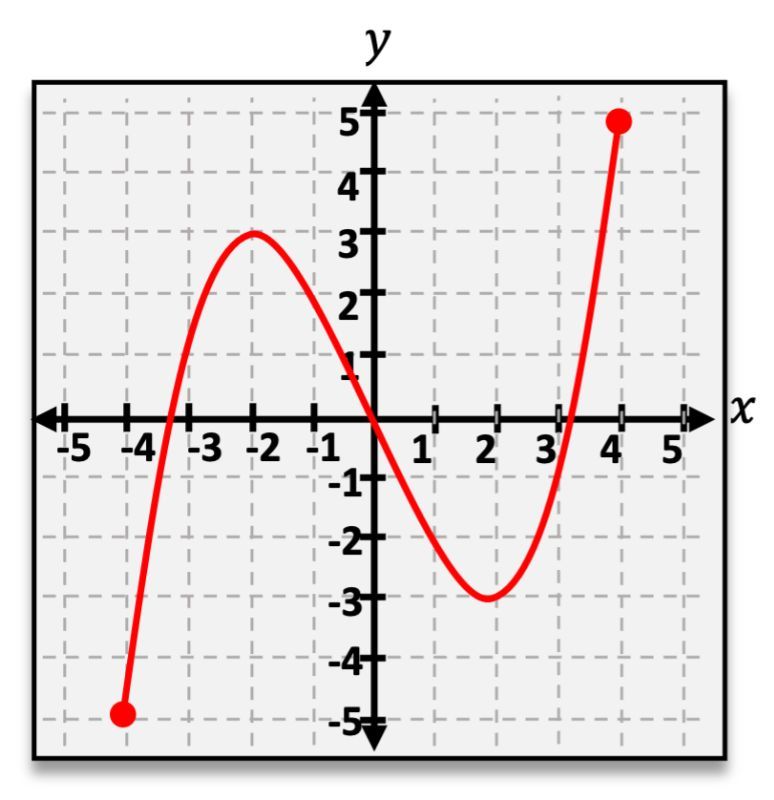
A more efficient method to assess whether a relation is a function is through the vertical line test. This test states that if a vertical line can be drawn on a graph that intersects the graph at more than one point, then the relation is not a function. Conversely, if every vertical line drawn intersects the graph at only one point, the relation is indeed a function.
For example, consider two graphs: the first graph fails the vertical line test, indicating that it is not a function, while the second graph passes the test, confirming it as a function. This method simplifies the process of determining the nature of relations and functions, making it easier to analyze complex graphs.
In summary, recognizing the difference between relations and functions, and applying the vertical line test, are key skills in understanding mathematical relationships and graphing. These concepts form the foundation for more advanced topics in mathematics, enhancing problem-solving abilities and analytical thinking.