In a population where only the total number of individuals with the dominant phenotype is known, how can you calculate the percentage of carriers and homozygous recessives?
Table of contents
- 1. Introduction to Genetics51m
- 2. Mendel's Laws of Inheritance3h 37m
- 3. Extensions to Mendelian Inheritance2h 41m
- 4. Genetic Mapping and Linkage2h 28m
- 5. Genetics of Bacteria and Viruses1h 21m
- 6. Chromosomal Variation1h 48m
- 7. DNA and Chromosome Structure56m
- 8. DNA Replication1h 10m
- 9. Mitosis and Meiosis1h 34m
- 10. Transcription1h 0m
- 11. Translation58m
- 12. Gene Regulation in Prokaryotes1h 19m
- 13. Gene Regulation in Eukaryotes44m
- 14. Genetic Control of Development44m
- 15. Genomes and Genomics1h 50m
- 16. Transposable Elements47m
- 17. Mutation, Repair, and Recombination1h 6m
- 18. Molecular Genetic Tools19m
- 19. Cancer Genetics29m
- 20. Quantitative Genetics1h 26m
- 21. Population Genetics50m
- 22. Evolutionary Genetics29m
21. Population Genetics
Hardy Weinberg
Problem 10d
Textbook Question
Consider a population in which the frequency of allele A is p = 0.7 and the frequency of allele a is q = 0.3 and where the alleles are codominant. What will be the allele frequencies after one generation if the following occurs?
wAA = 0.8, wAa = 1, waa = 0.8
 Verified step by step guidance
Verified step by step guidance1
Identify the initial allele frequencies: \(p = 0.7\) for allele \(A\) and \(q = 0.3\) for allele \(a\). Confirm that \(p + q = 1\).
Calculate the initial genotype frequencies under Hardy-Weinberg equilibrium using the formulas: \(f(AA) = p^2\), \(f(Aa) = 2pq\), and \(f(aa) = q^2\).
Apply the given fitness values to each genotype frequency to find the weighted genotype frequencies after selection: multiply each genotype frequency by its respective fitness value \(w_{AA} = 0.8\), \(w_{Aa} = 1\), and \(w_{aa} = 0.8\).
Calculate the mean fitness of the population, \(\bar{w}\), by summing the weighted genotype frequencies: \(\bar{w} = f(AA)w_{AA} + f(Aa)w_{Aa} + f(aa)w_{aa}\).
Normalize the weighted genotype frequencies by dividing each by \(\bar{w}\) to get the genotype frequencies after selection. Then, calculate the new allele frequencies after one generation using: \(p' = f'(AA) + \frac{1}{2}f'(Aa)\) and \(q' = f'(aa) + \frac{1}{2}f'(Aa)\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Allele Frequency
Allele frequency refers to how common an allele is in a population, expressed as a proportion or percentage. In this question, p and q represent the frequencies of alleles A and a, respectively, and their sum must equal 1. Understanding allele frequencies is essential for tracking genetic variation over generations.
Recommended video:
Guided course

New Alleles and Migration
Codominance
Codominance occurs when both alleles in a heterozygote are fully expressed, resulting in a phenotype that shows traits of both alleles simultaneously. Unlike dominance/recessiveness, neither allele masks the other. This affects how genotype frequencies translate into phenotypes and fitness values.
Recommended video:
Guided course
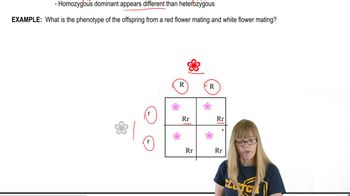
Variations on Dominance
Fitness and Selection Coefficients
Fitness (w) measures the reproductive success of a genotype relative to others, influencing allele frequency changes via natural selection. Here, different fitness values for AA, Aa, and aa genotypes affect survival and reproduction, altering allele frequencies in the next generation. Calculating post-selection frequencies requires weighting genotypes by their fitness.
Recommended video:
Guided course
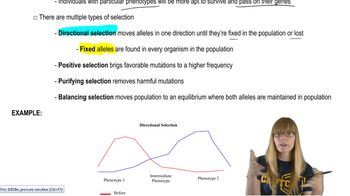
Natural Selection
Related Videos
Related Practice
Textbook Question
636
views


