Chi Square and Linkage: Videos & Practice Problems

The Chi Square test (χ²) is essential for assessing gene linkage by comparing observed and expected offspring ratios. In a cross of heterozygous organisms, if genes A and B are not linked, a 50% recombination frequency leads to expected ratios of 25 parental and 25 recombinant offspring. Calculating χ² involves the formula: χ2=((O-E)^2/E)). A p-value between 0.05 and 0.10 indicates acceptance of the null hypothesis, suggesting genes are not linked with 95% confidence.

Chi Square and Linkage

The Chi Square test is a statistical method used to determine the likelihood that two genes are linked based on observed and expected values. This analysis is particularly relevant in genetics when assessing gene linkage, which refers to the tendency of genes located close to each other on a chromosome to be inherited together. The Chi Square formula is expressed as:

\(\chi^2 = \sum \frac{(O - E)^2}{E}\)

where \(O\) represents the observed values and \(E\) represents the expected values. To conduct a Chi Square test for gene linkage, one must first establish the expected numbers of offspring based on the assumption that the genes are not linked. For two unlinked genes, the recombination frequency is typically around 50%, meaning that if 50 offspring are produced, one would expect approximately 25 parental and 25 recombinant offspring.

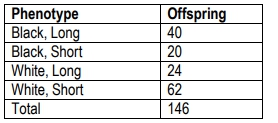
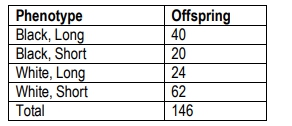
In a practical example, if a cross between two heterozygous organisms yields 31 parental and 19 recombinant offspring, the expected values would be 25 parental and 25 recombinant. The next step involves calculating the Chi Square value using the observed and expected numbers. In this case, the calculation yields a Chi Square value of 2.88.

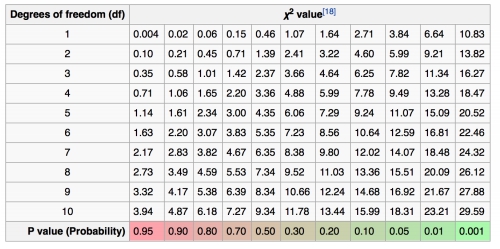
To interpret this value, one must determine the degrees of freedom, which in this scenario is calculated as the number of traits minus one. With two traits (parental and recombinant), the degrees of freedom is 1. Using a Chi Square distribution table, one can find the corresponding p-value, which indicates the probability of observing the data if the null hypothesis is true. In this case, the p-value falls between 0.05 and 0.10.

The null hypothesis posits that there is no significant difference between the observed and expected values, suggesting that the genes are not linked. Since the p-value is greater than 0.05, one would accept the null hypothesis, concluding that there is insufficient evidence to claim that the genes are linked. This analysis allows researchers to assert with 95% confidence that the genes are not linked, although it does not confirm linkage definitively. Further testing would be necessary to establish a more conclusive understanding of the genetic relationship between the two genes.

Black(B) rabbit coat colors are dominant to white(b) coat colors. Long hair (H) is dominant to short hair (h). A breeder crosses a rabbit homozygous for white, short hair with a homozygous black rabbit with long hair. The F1 is backcrossed to the rabbit with white, short hair and the following progeny are produced. Use the chi-square test to answer the following questions.

What are the expected offspring numbers if the two genes are not linked, and therefore assort independently?

• A. 73 parental, 73 recombinant
• B. 146 parental, 0 recombinant
• C. 60 parental, 86 recombinant
• D. 102 parental, 44 recombinant

Answer: (A)

Calculate the chi-square value for the above problem.

• A. 23.00
• B. 5.89
• C. 0.02
• D. 0.467

Answer: (A)

In this example, how many degrees of freedom should be used?

• A. 1
• B. 2
• C. 3
• D. 4

Answer: (A)

Using the appropriate chi-square value and degrees of freedom, do the coat color and hair length genes assort independently?

• A. Yes, both genes assort independently
• B. No, both genes do not assort independently (meaning they are linked)

Answer: (B)

Here’s what students ask on this topic:

What is the Chi Square test and how is it used in genetics?

The Chi Square test (χ²) is a statistical method used to determine if there is a significant difference between observed and expected frequencies. In genetics, it is often used to assess gene linkage by comparing the observed offspring ratios from a genetic cross to the expected ratios. The formula for the Chi Square test is:

${\chi }^2=\sum _{}^{}\frac{(O-E)2^{}}{E}$

where O is the observed frequency and E is the expected frequency. By calculating the χ² value and comparing it to a critical value from a χ² distribution table, researchers can determine if the observed differences are due to chance or if they suggest a linkage between genes.

How do you calculate the expected numbers in a Chi Square test for gene linkage?

To calculate the expected numbers in a Chi Square test for gene linkage, you first need to determine the recombination frequency if the genes are not linked. For unlinked genes, the recombination frequency is typically around 50%. This means you would expect 50% parental and 50% recombinant offspring. For example, if you have 50 offspring, you would expect 25 parental and 25 recombinant. These expected numbers are then used in the Chi Square formula to compare against the observed numbers from your genetic cross.

What does a p-value indicate in a Chi Square test for linkage?

A p-value in a Chi Square test for linkage indicates the probability that the observed differences between the expected and observed frequencies are due to chance. If the p-value is greater than 0.05, you accept the null hypothesis, suggesting that the genes are not linked. For example, a p-value between 0.05 and 0.10 means you can accept the null hypothesis with 95% confidence, indicating that the genes are likely not linked. Conversely, a p-value less than 0.05 would suggest rejecting the null hypothesis, implying potential linkage between the genes.

What is the null hypothesis in a Chi Square test for gene linkage?

The null hypothesis in a Chi Square test for gene linkage states that there is no significant difference between the observed and expected frequencies, implying that the genes are not linked. In other words, it assumes that any observed differences are due to random chance rather than a genetic linkage. If the Chi Square test results in a p-value greater than 0.05, the null hypothesis is accepted, suggesting that the genes are not linked. If the p-value is less than 0.05, the null hypothesis is rejected, indicating potential linkage.

How do you determine degrees of freedom in a Chi Square test for linkage?

Degrees of freedom in a Chi Square test for linkage are determined by the number of categories being compared minus one. For example, if you are comparing two categories (parental and recombinant offspring), the degrees of freedom would be 2 - 1 = 1. This value is used to find the critical value in the Chi Square distribution table, which helps determine the p-value and whether to accept or reject the null hypothesis.