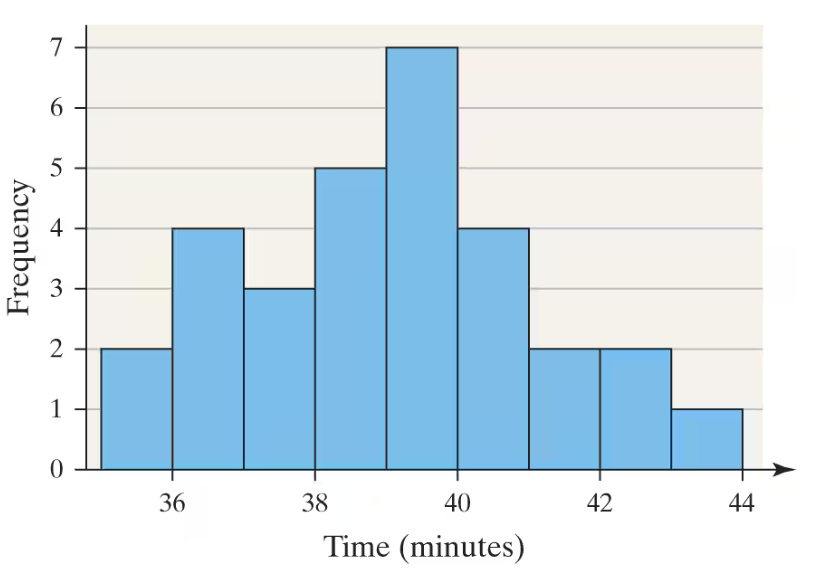
Download Time A histogram of the download time of a movie, in minutes, for 30 randomly selected movies is shown. The mean download time is 39.007 minutes and the median download time is 39.065 minutes. Identify the shape of the distribution. Which measure of central tendency better describes the “center” of the distribution?

Verified step by step guidance

1. Step 1: Examine the histogram to understand the shape of the distribution. Look at the symmetry of the bars around the center. In this histogram, the frequencies rise to a peak near the middle and then decrease roughly evenly on both sides, indicating a roughly symmetric distribution.
2. Step 2: Compare the mean and median values given: the mean download time is 39.007 minutes and the median download time is 39.065 minutes. Since these two measures of central tendency are very close to each other, this supports the observation that the distribution is symmetric.
3. Step 3: Recall that for symmetric distributions, the mean and median are approximately equal, and either can be used to describe the center. For skewed distributions, the median is usually preferred because it is less affected by extreme values.
4. Step 4: Based on the histogram's shape and the closeness of the mean and median, conclude that the distribution is roughly symmetric.
5. Step 5: Since the distribution is symmetric, the mean is a suitable measure of central tendency to describe the center of the distribution, but the median is also appropriate. In practice, the mean is often preferred for symmetric data.

Key Concepts

Shape of the Distribution

The shape of a distribution describes how data values are spread and can be symmetric, skewed left, or skewed right. A symmetric distribution has roughly equal frequencies on both sides of the center, while skewed distributions have a longer tail on one side. The histogram shows a roughly symmetric shape, indicating balanced data around the center.

Mean and Median as Measures of Central Tendency

Mean is the average of all data points, while median is the middle value when data is ordered. In symmetric distributions, mean and median are close or equal, making either a good measure of center. In skewed distributions, the median better represents the center as it is less affected by extreme values.

Interpreting Histograms

Histograms display data frequency across intervals, helping visualize distribution shape, spread, and central tendency. By examining bar heights and their arrangement, one can identify patterns like symmetry or skewness, which guide the choice of appropriate statistical measures.