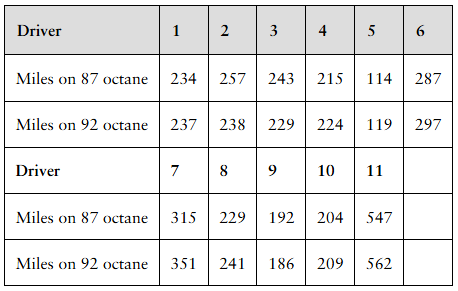
"[DATA] Does Octane Matter? Octane is a measure of how much fuel can be compressed before it spontaneously ignites. Some people believe that higher-octane fuels result in better gas mileage for their cars. To test this claim, a researcher randomly selected 11 individuals (and their cars) to participate in the study. Each participant received 10 gallons of gas and drove his or her car on a closed course that simulated both city and highway driving. The number of miles driven until the car ran out of gas was recorded. A coin flip was used to determine whether the car was filled up with 87-octane or 92-octane fuel first, and the driver did not know which type of fuel was in the tank. The results are in the following table:

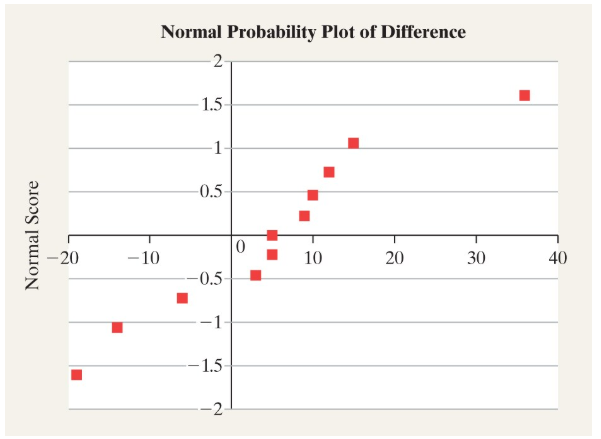
d. The differences are computed as “92 octane minus 87 octane.” The normal probability plot of the differences is shown in the next column. The correlation between the differenced data and the expected z-scores is 0.966. Is there reason to believe that the differences are normally distributed? Conclude that the differences can be normally distributed even though the original data are not.

Verified step by step guidance

1. Step 1: Understand the context and data. The problem involves paired data where each driver’s car is tested with two types of fuel (87 octane and 92 octane). The differences are calculated as '92 octane miles minus 87 octane miles' for each driver.
2. Step 2: Recognize the purpose of the normal probability plot. This plot is used to assess whether the differences follow a normal distribution by comparing the ordered differences to the expected z-scores from a normal distribution.
3. Step 3: Interpret the correlation value. The correlation between the differenced data and the expected z-scores is 0.966, which is very close to 1. This high correlation suggests that the differences closely follow a straight line on the normal probability plot, indicating approximate normality.
4. Step 4: Use the normal probability plot visual. The plot shows points that lie roughly along a straight line without large deviations or systematic patterns, reinforcing the conclusion that the differences can be considered normally distributed.
5. Step 5: Conclude based on the evidence. Even if the original data (miles driven on each fuel type separately) are not normally distributed, the differences between paired observations can be normally distributed. This justifies using statistical methods that assume normality of the differences.

Key Concepts

Paired Differences

Paired differences involve comparing two related measurements from the same subject or entity, such as miles driven on 92-octane versus 87-octane fuel for the same driver. This approach controls for individual variability, allowing a more precise assessment of the effect of the treatment or condition.

Normality Assumption in Paired Differences

Many statistical tests, like the paired t-test, assume that the differences between paired observations are approximately normally distributed. This assumption can be checked using a normal probability plot, where data points closely following a straight line indicate approximate normality.

Correlation in Normal Probability Plot

The correlation between ordered differences and expected z-scores in a normal probability plot quantifies how well the data fit a normal distribution. A high correlation (close to 1) suggests the differences are normally distributed, justifying the use of parametric tests even if the original data are not normal.