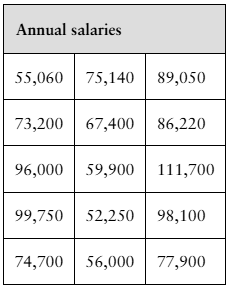
In Exercises 15–22, test the claim about the population variance or standard deviation at the level of significance Assume the population is normally distributed.
Claim: σ<40, α=0.01 . Sample statistics: s=40.8, n=12
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

