Salary Offers You are applying for jobs at two companies. Company C offers starting salaries with μ = \$59,000 and σ = \$1500. Company D offers starting salaries with μ = \$59,000 and σ = \$1000. From which company are you more likely to get an offer of \$62,000 or more? Explain your reasoning.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 56m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - ExcelBonus23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - ExcelBonus28m
- Confidence Intervals for Population Means - ExcelBonus25m
- 8. Sampling Distributions & Confidence Intervals: Proportion2h 10m
- 9. Hypothesis Testing for One Sample5h 8m
- Steps in Hypothesis Testing1h 6m
- Performing Hypothesis Tests: Means1h 4m
- Hypothesis Testing: Means - ExcelBonus42m
- Performing Hypothesis Tests: Proportions37m
- Hypothesis Testing: Proportions - ExcelBonus27m
- Performing Hypothesis Tests: Variance12m
- Critical Values and Rejection Regions28m
- Link Between Confidence Intervals and Hypothesis Testing12m
- Type I & Type II Errors16m
- 10. Hypothesis Testing for Two Samples5h 37m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - ExcelBonus28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - ExcelBonus12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - ExcelBonus9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - ExcelBonus21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - ExcelBonus12m
- Two Variances and F Distribution29m
- Two Variances - Graphing CalculatorBonus16m
- 11. Correlation1h 24m
- 12. Regression3h 33m
- Linear Regression & Least Squares Method26m
- Residuals12m
- Coefficient of Determination12m
- Regression Line Equation and Coefficient of Determination - ExcelBonus8m
- Finding Residuals and Creating Residual Plots - ExcelBonus11m
- Inferences for Slope31m
- Enabling Data Analysis ToolpakBonus1m
- Regression Readout of the Data Analysis Toolpak - ExcelBonus21m
- Prediction Intervals13m
- Prediction Intervals - ExcelBonus19m
- Multiple Regression - ExcelBonus29m
- Quadratic Regression15m
- Quadratic Regression - ExcelBonus10m
- 13. Chi-Square Tests & Goodness of Fit2h 21m
- 14. ANOVA2h 28m
3. Describing Data Numerically
Interpreting Standard Deviation
Problem 2.4.45
Textbook Question
Comparing Variation in Different Data Sets In Exercises 45–50, find the coefficient of variation for each of the two data sets. Then compare the results.
Annual Salaries Sample annual salaries (in thousands of dollars) for entry level architects in Denver, CO, and Los Angeles, CA, are listed.
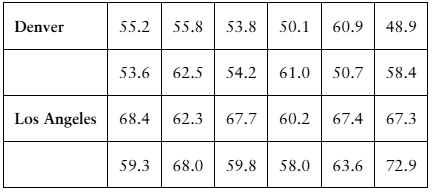
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the coefficient of variation (CV). The CV is a measure of relative variability and is calculated as the ratio of the standard deviation (SD) to the mean (μ), expressed as a percentage: CV = (SD / μ) × 100.
Step 2: Calculate the mean (μ) for each data set. Add all the values in the Denver data set and divide by the number of values to find the mean for Denver. Repeat the process for the Los Angeles data set.
Step 3: Calculate the standard deviation (SD) for each data set. Use the formula for SD: SD = sqrt(Σ(xᵢ - μ)² / (n - 1)), where xᵢ represents each data point, μ is the mean, and n is the number of data points. Perform this calculation for both Denver and Los Angeles data sets.
Step 4: Compute the coefficient of variation (CV) for each data set using the formula CV = (SD / μ) × 100. Substitute the mean and standard deviation values calculated in the previous steps for both Denver and Los Angeles.
Step 5: Compare the CVs of the two data sets. The data set with the higher CV has greater relative variability in annual salaries.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Coefficient of Variation
The coefficient of variation (CV) is a statistical measure of the relative variability of a data set. It is calculated as the ratio of the standard deviation to the mean, expressed as a percentage. A higher CV indicates greater dispersion relative to the mean, making it useful for comparing the degree of variation between different data sets, especially when the means are significantly different.
Recommended video:
Guided course

Coefficient of Determination
Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. It quantifies how much the individual data points deviate from the mean of the data set. A low standard deviation indicates that the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range of values.
Recommended video:
Guided course

Calculating Standard Deviation
Mean
The mean, or average, is a measure of central tendency that is calculated by summing all the values in a data set and dividing by the number of values. It provides a single value that represents the center of the data distribution. The mean is sensitive to extreme values (outliers), which can skew the results, making it important to consider alongside other measures of central tendency and variability.
Recommended video:
Guided course

Calculating the Mean
Related Videos
Related Practice
Textbook Question
84
views


