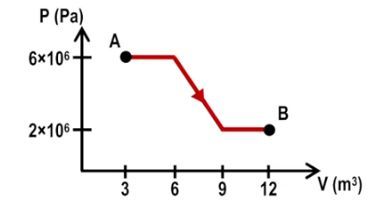
In thermodynamics, calculating the work done during multiple processes is essential for understanding energy transfer within a system. When a system transitions through various states, such as from point A to point B and then from point B to point C, the total work done can be determined by summing the work from each individual process. For instance, if the work done from A to B is 100 joules and from B to C is 80 joules, the total work done is simply the sum: 100 + 80 = 180 joules.
The general formula for total work done over multiple processes is expressed as:
\[W_{\text{total}} = W_1 + W_2 + \ldots + W_n\]
In many scenarios, you will need to calculate the work for each process based on specific thermodynamic conditions. There are four primary types of thermodynamic processes that frequently arise: isobaric, isovolumetric (or isochoric), isothermal, and adiabatic. This summary will focus on isobaric and isovolumetric processes.
An isobaric process occurs at constant pressure. In a PV diagram, this is represented by a horizontal line. The work done during an isobaric process can be calculated using the equation:
\[W = P \Delta V\]
where \(P\) is the constant pressure and \(\Delta V\) is the change in volume.
Conversely, an isovolumetric process maintains constant volume, which means there is no change in volume (\(\Delta V = 0\)). This is depicted as a vertical line on a PV diagram. Since there is no volume change, the work done in an isovolumetric process is:
\[W = 0\]
To illustrate these concepts, consider a system transitioning from point A to point C via two different paths: A to B to C and A to D to C. In the first path, the segment from A to B is isobaric, while from B to C is isovolumetric. The work done from A to B can be calculated using the isobaric formula, while the work from B to C is zero due to the isovolumetric nature. Thus, the total work for this path is simply the work from A to B.
In the second path, A to D is isovolumetric (resulting in zero work), and D to C is isobaric. Here, the total work is solely determined by the work done from D to C. This demonstrates that the work done between two states is path-dependent, meaning it varies based on the specific route taken through the thermodynamic processes.
Understanding these principles is crucial for solving complex thermodynamic problems and analyzing energy changes in various systems.