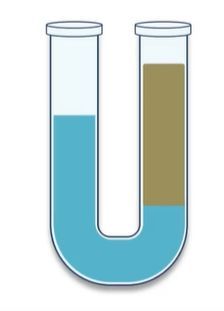
In this discussion, we explore the U-shaped tube, a common type of pressure gauge used to measure pressure differences by utilizing the height of liquid columns. The fundamental principle behind this device is that pressure is determined by the height difference of the liquid columns, which can be expressed using the equation:
\( P_{\text{bottom}} = P_{\text{top}} + \rho g h \)
In a U-shaped tube, both ends can be open to the atmosphere or one end can be closed, creating a vacuum. When both ends are open, the liquid levels will equalize due to atmospheric pressure acting equally on both sides. However, if one side is closed and a vacuum is created, the liquid will rise higher on the open side due to the atmospheric pressure pushing down on it.
When dealing with two different liquids in the U-tube, the situation becomes more complex. The heights of the two liquid columns will not equalize directly because they have different densities. The pressure at the interface of the two liquids must be equal, leading to the relationship:
\( \rho_1 h_1 = \rho_2 h_2 \)
Here, \( \rho_1 \) and \( \rho_2 \) are the densities of the first and second liquids, while \( h_1 \) and \( h_2 \) are their respective heights. This equation is crucial for solving problems involving U-shaped tubes with two different liquids.
To find the difference in height between the two liquid columns, we can use the equation:
\( \Delta h = |h_2 - h_1| \)
In practical applications, such as calculating gauge pressure at the interface of two liquids, the gauge pressure can be determined using the formula:
\( P_{\text{gauge}} = \rho g h \)
Where \( \rho \) is the density of the liquid above the point of interest, \( g \) is the acceleration due to gravity, and \( h \) is the height of the liquid column. For example, if we have a column of oil above water, we would use the density of the oil and its height to calculate the gauge pressure at the water-oil interface.
In summary, understanding the principles of pressure in U-shaped tubes involves recognizing how different liquid densities affect height differences and pressure calculations. The key equations allow for the determination of gauge pressure and height differences, which are essential for solving related physics problems.