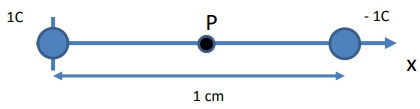
To determine the point along the X-axis where the electric field is zero due to two charges, one positive and one negative, we need to analyze the behavior of electric fields produced by these charges. Positive charges generate electric field lines that radiate outward, while negative charges create electric field lines that point inward toward the charge. In this scenario, we have a positive charge (2 Coulombs) and a negative charge (3 Coulombs) positioned on the X-axis.
We begin by identifying potential regions where the electric fields from both charges could cancel each other out. The three regions to consider are to the left of the positive charge, between the two charges, and to the right of the negative charge. In the middle region, the electric field from the positive charge points to the right, while the electric field from the negative charge also points to the right, meaning they will always add together rather than cancel out. Therefore, the middle region cannot be the location where the electric field is zero.
Next, we examine the right region. Here, the electric field from the positive charge still points outward (to the right), while the electric field from the negative charge points inward (to the left). However, due to the larger magnitude of the negative charge and its proximity, the electric field from the negative charge will always be greater than that from the positive charge, preventing cancellation in this region as well.
Thus, we focus on the left region, where it is possible for the electric fields to balance out. We denote the distance from the positive charge to the point of interest as \(X\). The condition for the electric fields to cancel is that the magnitudes of the electric fields from both charges must be equal and opposite. The electric field \(E\) due to a point charge is given by the formula:
\(E = k \frac{Q}{r^2}\
where \(k\) is Coulomb's constant, \(Q\) is the charge, and \(r\) is the distance from the charge to the point of interest. For the positive charge, the electric field at distance \(X\) is:
\(E_{+} = k \frac{2}{X^2}\
For the negative charge, the distance to the point of interest is \(X + 0.7\) meters (since the negative charge is 0.7 meters to the right of the positive charge), and its electric field is:
\(E_{-} = k \frac{3}{(X + 0.7)^2}\
Setting the magnitudes equal gives us:
\(k \frac{2}{X^2} = k \frac{3}{(X + 0.7)^2}\
We can cancel \(k\) from both sides, leading to:
\(\frac{2}{X^2} = \frac{3}{(X + 0.7)^2}\
Cross-multiplying yields:
2 \((X + 0.7)^2 = 3X^2\
Expanding and rearranging gives:
2(X^2 + 1.4X + 0.49) = 3X^2\
2X^2 + 2.8X + 0.98 = 3X^2\
0 = X^2 - 2.8X - 0.98\
To solve for \(X\), we can use the quadratic formula:
\(X = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\
where \(a = 1\), \(b = -2.8\), and \(c = -0.98\). Plugging in these values gives:
\(X = \frac{2.8 \pm \sqrt{(-2.8)^2 - 4(1)(-0.98)}}{2(1)}\
Calculating the discriminant:
\(X = \frac{2.8 \pm \sqrt{7.84 + 3.92}}{2}\
\(X = \frac{2.8 \pm \sqrt{11.76}}{2}\
\(X = \frac{2.8 \pm 3.43}{2}\
This results in two potential solutions for \(X\): one positive and one negative. The negative solution indicates a position to the left of the positive charge. After calculations, we find:
\(X \approx -0.31\) meters, or -31 centimeters.
Thus, the point where the electric field is zero is located 31 centimeters to the left of the positive charge.