"Putting It Together: Red-Light Cameras
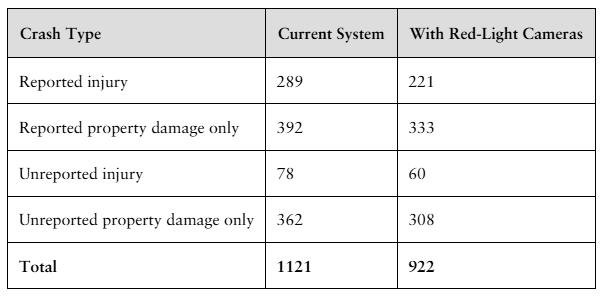
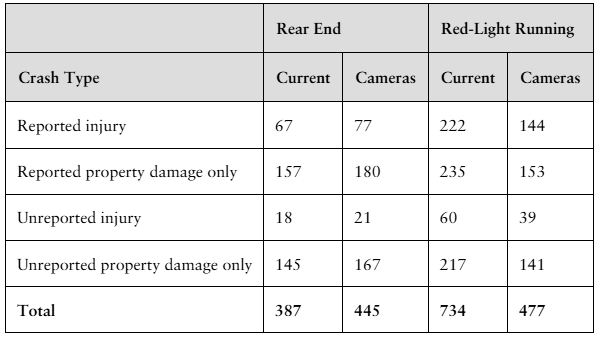
In a study of the feasibility of a red-light camera program in the city of Milwaukee, the data below summarize the projected number of crashes at 13 selected intersections over a five-year period.
(g) Based on the data shown, does it appear that the red-light camera program will be beneficial in reducing crashes at the intersections? Explain.
"

Verified step by step guidance

1. Step 1: Understand the data provided. The first table shows the total number of crashes over five years at 13 intersections under the current system and with red-light cameras. The second table breaks down these crashes into two categories: Rear End and Red-Light Running, with counts for both the current system and with cameras.
2. Step 2: Compare the total number of crashes in the first table. Note the total crashes under the current system (1121) and with red-light cameras (922). This comparison gives an initial indication of whether the cameras reduce overall crashes.
3. Step 3: Analyze the breakdown in the second table. For Rear End crashes, compare the totals under the current system (387) and with cameras (445). For Red-Light Running crashes, compare the totals under the current system (734) and with cameras (477). This helps identify which type of crashes increase or decrease with the cameras.
4. Step 4: Consider the nature of the crashes. Red-Light Running crashes are generally more dangerous than Rear End crashes. Even if Rear End crashes increase, a reduction in Red-Light Running crashes might still indicate a safety benefit.
5. Step 5: Summarize your findings by weighing the reduction in total crashes and the changes in crash types. Use this to explain whether the red-light camera program appears beneficial in reducing crashes and improving safety at the intersections.

Key Concepts

Comparative Data Analysis

Comparative data analysis involves examining two or more data sets to identify differences or trends. In this context, comparing crash numbers under the current system versus with red-light cameras helps determine if the intervention reduces crashes. Understanding how to interpret these differences is crucial for evaluating program effectiveness.

Descriptive Statistics

Descriptive statistics summarize and describe features of a data set, such as totals and category breakdowns. Here, totals of crashes and their types provide a clear overview of the situation before and after implementing red-light cameras, enabling straightforward comparison and insight into the program's impact.

Causation vs. Correlation

Distinguishing causation from correlation is essential when interpreting data. A reduction in crashes with red-light cameras suggests a correlation, but other factors might influence results. Understanding this helps avoid overestimating the program's effect without further controlled studies.