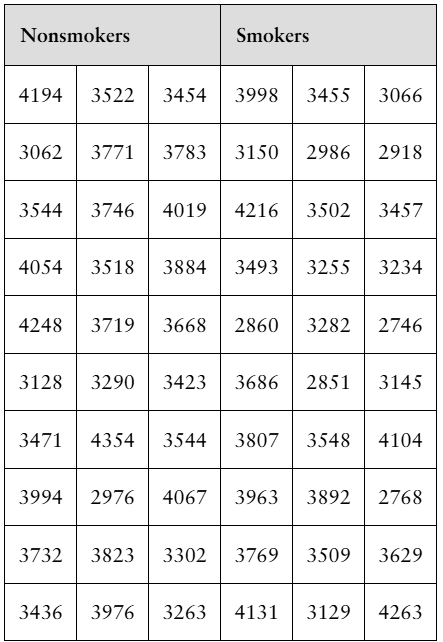
"[DATA] Putting It Together: Paternal Smoking It is well-documented that active maternal smoking during pregnancy is associated with lower-birth-weight babies. Researchers wanted to determine if there is a relationship between paternal smoking habits and birth weight. The researchers administered a questionnaire to each parent of newborn infants. One question asked whether the individual smoked regularly. Because the survey was administered within 15 days of birth, it was assumed that any regular smokers were also regular smokers during pregnancy. Birth weights for the babies (in grams) of nonsmoking mothers were obtained and divided into two groups, nonsmoking fathers and smoking fathers. The given data are representative of the data collected by the researchers. The researchers concluded that the birth weight of babies whose father smoked was less than the birth weight of babies whose father did not smoke.


f. Interpret the first quartile for both the nonsmoker and smoker group."

Verified step by step guidance

1. Step 1: Understand what the first quartile (Q1) represents. The first quartile is the value below which 25% of the data fall. It is a measure of the lower spread of the data and helps to understand the distribution of birth weights in each group.
2. Step 2: Organize the birth weight data for each group (Nonsmokers and Smokers) in ascending order. This is necessary to accurately find the position of the first quartile in the sorted data set.
3. Step 3: Determine the position of the first quartile in each sorted data set using the formula: \(Q1 = \frac{1}{4} (n + 1)\), where \(n\) is the number of data points in the group. This gives the rank or position of the first quartile value.
4. Step 4: Locate the first quartile value in each sorted list by finding the data point at the position calculated in Step 3. If the position is not an integer, interpolate between the two closest data points.
5. Step 5: Interpret the first quartile values for both groups by explaining what these values mean in the context of birth weights. For example, the first quartile for nonsmokers indicates that 25% of babies born to nonsmoking fathers have birth weights below this value, and similarly for the smoker group.

Key Concepts

Quartiles and the First Quartile (Q1)

Quartiles divide a data set into four equal parts after sorting the data. The first quartile (Q1) is the value below which 25% of the data fall. It helps describe the lower spread of the data and is useful for understanding the distribution and identifying potential outliers.

Comparing Distributions Between Groups

When comparing two groups, such as nonsmoking and smoking fathers, analyzing quartiles helps understand differences in data spread and central tendency. Comparing Q1 values shows how the lower 25% of birth weights differ between groups, indicating potential effects of paternal smoking.

Interpreting Birth Weight Data in Context

Birth weight data reflect newborn health and can be influenced by parental factors. Interpreting quartiles in this context means understanding what a specific quartile value implies about the baby's weight relative to others, helping assess the impact of paternal smoking on infant health outcomes.