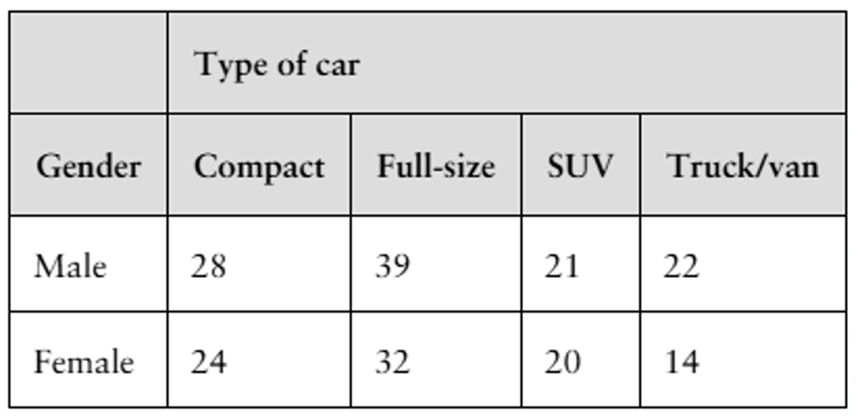
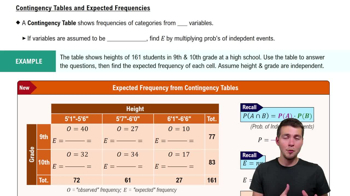
Consider the following contingency table, which relates the number of applicants accepted to a college and gender.
c. What might you conclude about the admittance policies of the school? A lurking variable is the type of school applied to. This particular college has two programs of study: business and social work. The following table shows applications by type of school.