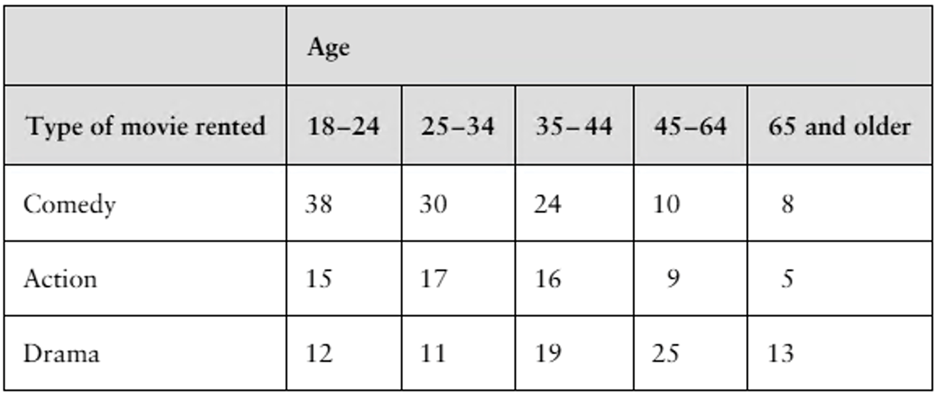
Consider the following contingency table, which relates the number of applicants accepted to a college and gender.
f. Explain carefully how the bias disappears when type of school is considered.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 8:18m
8:18mMaster Contingency Tables & Expected Frequencies with a bite sized video explanation from Patrick
Start learning