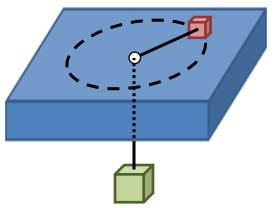
In this scenario, we explore the conservation of angular momentum through a system where a block spins on a horizontal table, connected to a hanging mass via a string that passes through a hole in the table. The block's motion is influenced by the tension in the string, which provides the necessary centripetal force for circular motion. As the length of the string decreases, the radius of the block's circular path also decreases, leading to an increase in its angular velocity.
Initially, the block has a mass of 2 kg and spins at 120 RPM when it is 10 cm (0.1 m) from the hole. To find the new RPM when the radius is reduced to 6 cm (0.06 m), we apply the principle of conservation of angular momentum, which states that the initial angular momentum equals the final angular momentum. This can be expressed mathematically as:
\[I_{\text{initial}} \omega_{\text{initial}} = I_{\text{final}} \omega_{\text{final}}\]
For a point mass, the moment of inertia \(I\) is given by \(m r^2\). Since we are working with RPM, we convert angular velocity \(\omega\) to RPM using the relationship:
\[\omega = \frac{2 \pi \text{RPM}}{60}\]
After substituting and simplifying, we arrive at the equation:
\[\text{RPM}_{\text{final}} = \text{RPM}_{\text{initial}} \left(\frac{r_{\text{initial}}^2}{r_{\text{final}}^2}\right)\]
Plugging in the values, we find that the new RPM is approximately 333 RPM, indicating that the block spins faster as the radius decreases.
Next, we calculate the linear tangential speed \(v_{\text{tan}}\) at this new RPM. The relationship between tangential speed and angular velocity is given by:
\[v_{\text{tan}} = r \omega\]
Substituting the new radius and the converted angular velocity, we find that the tangential speed is approximately 2.1 m/s.
Finally, to maintain the block's spinning at the new RPM, we need to determine the mass \(m_2\) of the hanging object. The tension in the string, which provides the centripetal force, is equal to the weight of the hanging mass:
\[T = m_2 g\]
Using the centripetal force equation, we can express this as:
\[T = m_1 \frac{v_{\text{tan}}^2}{r}\]
By equating the two expressions for tension and solving for \(m_2\), we find:
\[m_2 = \frac{m_1 v_{\text{tan}}^2}{g r}\]
Substituting the known values, we determine that \(m_2\) must be approximately 15 kg to maintain the block's spinning at the calculated RPM. This example illustrates the interconnectedness of angular momentum, centripetal force, and the effects of changing radius on rotational motion.