Understanding capacitor circuits involves mastering the concepts of equivalent capacitance, charge, and voltage across capacitors in both series and parallel configurations. In series connections, the equivalent capacitance can be calculated using the inverse sum rule, which states that the inverse of the equivalent capacitance (\(C_{EQ}\)) is equal to the sum of the inverses of the individual capacitances:
\[\frac{1}{C_{EQ}} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots + \frac{1}{C_n}\]
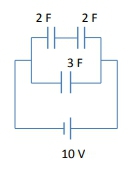
In a series circuit, all capacitors share the same charge. For example, if one capacitor has a charge of 3 coulombs, all capacitors in that series will also have 3 coulombs. This shared charge is crucial for analyzing the circuit.
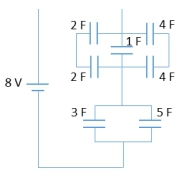
On the other hand, in parallel connections, the equivalent capacitance is simply the sum of the individual capacitances:
\[C_{EQ} = C_1 + C_2 + \ldots + C_n\]
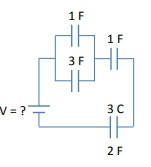
In parallel circuits, capacitors share the same voltage across their terminals. For instance, if one capacitor has a voltage of 2 volts, all capacitors in that parallel configuration will also have 2 volts across them. This distinction between charge and voltage sharing is essential for solving problems involving mixed configurations of capacitors.
To solve capacitor circuit problems, follow a systematic approach. First, determine the equivalent capacitance of the entire circuit. Once you have \(C_{EQ}\), you can find the total charge (\(Q\)) using the relationship:
\[Q = C \times V\]
Where \(V\) is the total voltage supplied by the battery. After calculating the total charge, you can work backwards to find the charge and voltage across each individual capacitor. For capacitors in series, remember that they all have the same charge, while for capacitors in parallel, they will have the same voltage.
For example, if you have a circuit with a 6 farad capacitor in series with a parallel combination of a 1 farad and a 2 farad capacitor, you would first calculate the equivalent capacitance of the parallel capacitors (which would be 3 farads), then find the total equivalent capacitance of the series combination (which would be 2 farads). With the total voltage known, you can find the total charge and subsequently the individual voltages and charges across each capacitor.
By organizing your calculations and keeping track of the relationships between charge, capacitance, and voltage, you can effectively analyze and solve complex capacitor circuit problems.