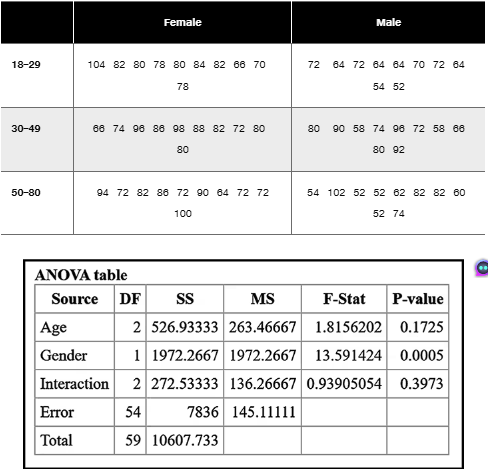
Pulse Rates Shown below are pulse rates from Data Set 1 “Body Data” in Appendix B, and the StatCrunch display from two-way analysis of variance of these data. In analyzing these data, what important feature is addressed with two-way analysis of variance that is not addressed with two separate tests of (1) difference between mean pulse rates based on gender, or (2) differences among the mean pulse rates in the different age brackets?

Verified step by step guidance

1. Step 1: Understand the purpose of two-way ANOVA. Two-way analysis of variance (ANOVA) is used to examine the effect of two different categorical independent variables (factors) on a continuous dependent variable, and also to check if there is an interaction effect between these two factors.
2. Step 2: Identify the factors in the problem. Here, the two factors are 'Age' (with three groups: 18-29, 30-49, 50-80) and 'Gender' (with two groups: Female and Male). The dependent variable is the pulse rate.
3. Step 3: Recognize what separate tests would do. Conducting separate tests for (1) difference between mean pulse rates based on gender and (2) differences among mean pulse rates in different age brackets would only analyze the main effects independently, ignoring any possible interaction between age and gender.
4. Step 4: Understand the interaction term in two-way ANOVA. The interaction term tests whether the effect of one factor (e.g., gender) on pulse rate depends on the level of the other factor (e.g., age group). This is an important feature that separate one-way ANOVAs or t-tests cannot detect.
5. Step 5: Conclude the importance of two-way ANOVA. By using two-way ANOVA, you can simultaneously test for the main effects of age and gender and also determine if there is a significant interaction effect between age and gender on pulse rates, providing a more comprehensive analysis.

Key Concepts

Two-Way Analysis of Variance (ANOVA)

Two-way ANOVA is a statistical method used to examine the effect of two independent categorical variables on a continuous dependent variable simultaneously. It allows testing for main effects of each factor and their interaction effect, providing a more comprehensive analysis than separate one-way ANOVAs.

Interaction Effect

The interaction effect in two-way ANOVA tests whether the effect of one factor depends on the level of the other factor. This is important because it reveals if the combined influence of factors differs from their individual effects, which cannot be detected by separate tests.

Main Effects vs. Interaction

Main effects refer to the individual impact of each factor (e.g., age or gender) on the response variable, while interaction effects show how factors jointly influence the response. Two-way ANOVA distinguishes these effects, unlike separate tests that only assess main effects independently.