Table of contents
- 1. Introduction to Accounting1h 21m
- 2. Transaction Analysis1h 13m
- 3. Accrual Accounting Concepts2h 38m
- Accrual Accounting vs. Cash Basis Accounting10m
- Revenue Recognition and Expense Recognition24m
- Introduction to Adjusting Journal Entries and Prepaid Expenses36m
- Adjusting Entries: Supplies12m
- Adjusting Entries: Unearned Revenue11m
- Adjusting Entries: Accrued Expenses12m
- Adjusting Entries: Accrued Revenues6m
- Adjusting Entries: Depreciation16m
- Summary of Adjusting Entries7m
- Unadjusted vs Adjusted Trial Balance6m
- Closing Entries10m
- Post-Closing Trial Balance2m
- 4. Merchandising Operations2h 30m
- Service Company vs. Merchandising Company10m
- Net Sales28m
- Cost of Goods Sold - Perpetual Inventory vs. Periodic Inventory9m
- Perpetual Inventory - Purchases10m
- Perpetual Inventory - Freight Costs9m
- Perpetual Inventory - Purchase Discounts11m
- Perpetual Inventory - Purchasing Summary6m
- Periodic Inventory - Purchases14m
- Periodic Inventory - Freight Costs7m
- Periodic Inventory - Purchase Discounts10m
- Periodic Inventory - Purchasing Summary6m
- Single-step Income Statement4m
- Multi-step Income Statement17m
- Comprehensive Income2m
- 5. Inventory1h 55m
- Merchandising Company vs. Manufacturing Company6m
- Physical Inventory Count, Ownership of Goods, and Consigned Goods10m
- Specific Identification7m
- Periodic Inventory - FIFO, LIFO, and Average Cost23m
- Perpetual Inventory - FIFO, LIFO, and Average Cost31m
- Financial Statement Effects of Inventory Costing Methods10m
- Lower of Cost or Market11m
- Inventory Errors14m
- 6. Internal Controls and Reporting Cash1h 16m
- 7. Receivables and Investments3h 8m
- Types of Receivables8m
- Net Accounts Receivable: Direct Write-off Method5m
- Net Accounts Receivable: Allowance for Doubtful Accounts13m
- Net Accounts Receivable: Percentage of Sales Method9m
- Net Accounts Receivable: Aging of Receivables Method11m
- Notes Receivable25m
- Introduction to Investments in Securities13m
- Trading Securities31m
- Available-for-Sale (AFS) Securities26m
- Held-to-Maturity (HTM) Securities17m
- Equity Method25m
- 8. Long Lived Assets5h 1m
- Initial Cost of Long Lived Assets42m
- Basket (Lump-sum) Purchases13m
- Ordinary Repairs vs. Capital Improvements10m
- Depreciation: Straight Line32m
- Depreciation: Declining Balance29m
- Depreciation: Units-of-Activity28m
- Depreciation: Summary of Main Methods8m
- Depreciation for Partial Years13m
- Retirement of Plant Assets (No Proceeds)14m
- Sale of Plant Assets18m
- Change in Estimate: Depreciation21m
- Intangible Assets and Amortization17m
- Natural Resources and Depletion16m
- Asset Impairments16m
- Exchange for Similar Assets16m
- 9. Current Liabilities2h 19m
- 10. Time Value of Money1h 23m
- 11. Long Term Liabilities2h 45m
- 12. Stockholders' Equity2h 15m
- Characteristics of a Corporation17m
- Shares Authorized, Issued, and Outstanding9m
- Issuing Par Value Stock12m
- Issuing No Par Value Stock5m
- Issuing Common Stock for Assets or Services8m
- Retained Earnings14m
- Retained Earnings: Prior Period Adjustments9m
- Preferred Stock11m
- Treasury Stock9m
- Dividends and Dividend Preferences17m
- Stock Dividends10m
- Stock Splits9m
- 13. Statement of Cash Flows2h 24m
- 14. Financial Statement Analysis5h 25m
- Horizontal Analysis14m
- Vertical Analysis23m
- Common-sized Statements5m
- Trend Percentages7m
- Discontinued Operations and Extraordinary Items6m
- Introduction to Ratios8m
- Ratios: Earnings Per Share (EPS)10m
- Ratios: Working Capital and the Current Ratio14m
- Ratios: Quick (Acid Test) Ratio12m
- Ratios: Gross Profit Rate9m
- Ratios: Profit Margin7m
- Ratios: Quality of Earnings Ratio8m
- Ratios: Inventory Turnover10m
- Ratios: Average Days in Inventory9m
- Ratios: Accounts Receivable (AR) Turnover9m
- Ratios: Average Collection Period (Days Sales Outstanding)8m
- Ratios: Return on Assets (ROA)8m
- Ratios: Total Asset Turnover5m
- Ratios: Fixed Asset Turnover5m
- Ratios: Profit Margin x Asset Turnover = Return On Assets9m
- Ratios: Accounts Payable Turnover6m
- Ratios: Days Payable Outstanding (DPO)8m
- Ratios: Times Interest Earned (TIE)7m
- Ratios: Debt to Asset Ratio5m
- Ratios: Debt to Equity Ratio5m
- Ratios: Payout Ratio5m
- Ratios: Dividend Yield Ratio7m
- Ratios: Return on Equity (ROE)10m
- Ratios: DuPont Model for Return on Equity (ROE)20m
- Ratios: Free Cash Flow10m
- Ratios: Price-Earnings Ratio (PE Ratio)7m
- Ratios: Book Value per Share of Common Stock7m
- Ratios: Cash to Monthly Cash Expenses8m
- Ratios: Cash Return on Assets7m
- Ratios: Economic Return from Investing6m
- Ratios: Capital Acquisition Ratio6m
- 15. GAAP vs IFRS56m
- GAAP vs. IFRS: Introduction7m
- GAAP vs. IFRS: Classified Balance Sheet6m
- GAAP vs. IFRS: Recording Differences4m
- GAAP vs. IFRS: Adjusting Entries4m
- GAAP vs. IFRS: Merchandising3m
- GAAP vs. IFRS: Inventory3m
- GAAP vs. IFRS: Fraud, Internal Controls, and Cash3m
- GAAP vs. IFRS: Receivables2m
- GAAP vs. IFRS: Long Lived Assets5m
- GAAP vs. IFRS: Liabilities3m
- GAAP vs. IFRS: Stockholders' Equity3m
- GAAP vs. IFRS: Statement of Cash Flows5m
- GAAP vs. IFRS: Analysis and Income Statement Presentation5m
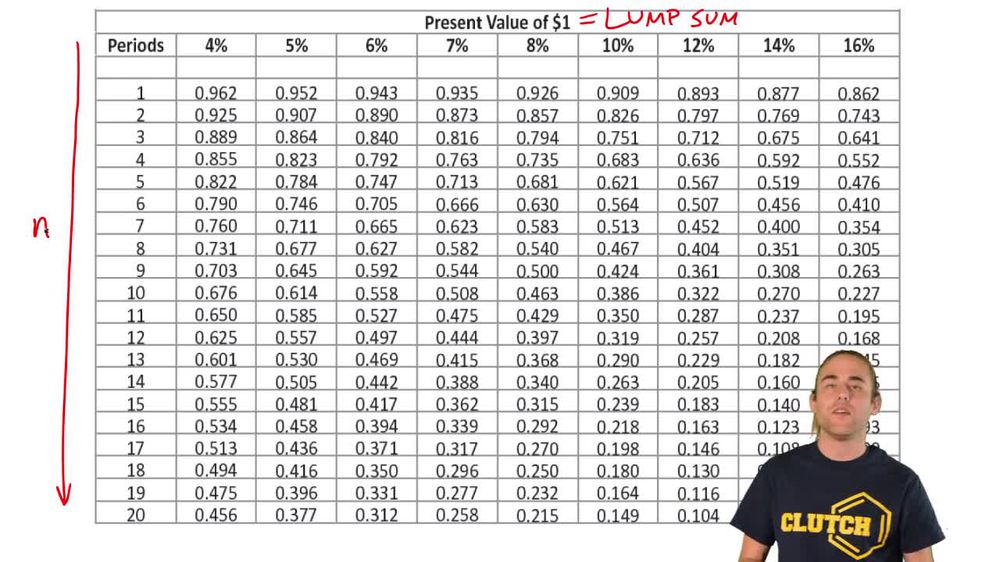
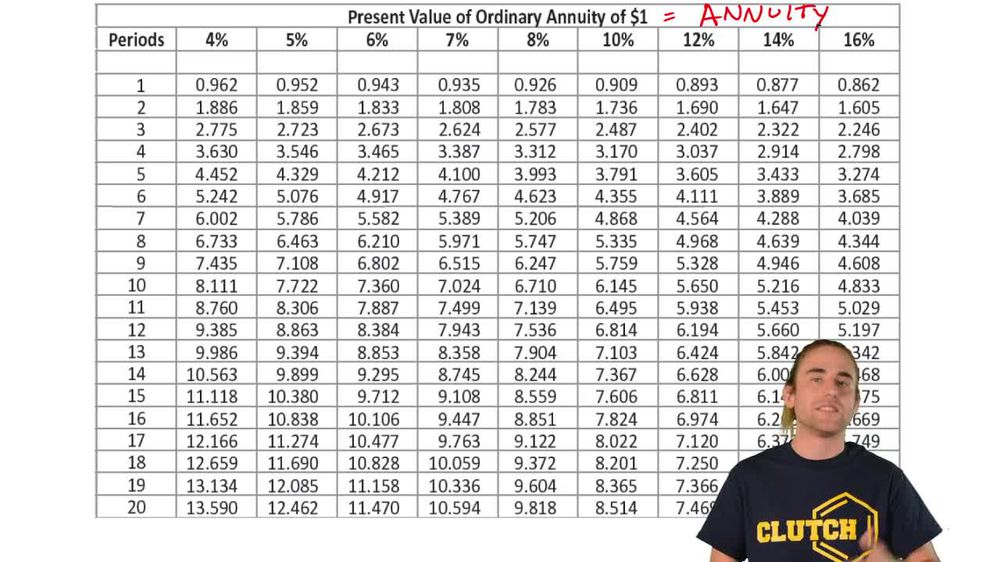
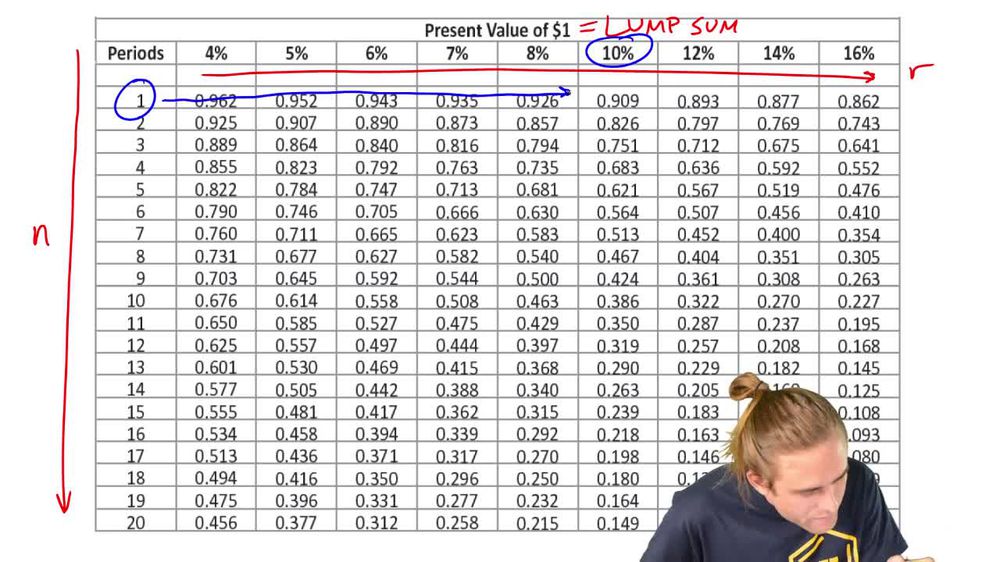
10. Time Value of Money
Using Time Value of Money Tables
Struggling with Financial Accounting?
Join thousands of students who trust us to help them ace their exams!Watch the first video
TVM Tables and Bonds Payable
Brian Krogol
Video duration:
12mPlay a video:
Related Videos
Related Practice