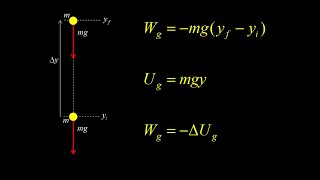Table of contents
- 0. Math Review31m
- 1. Intro to Physics Units1h 29m
- 2. 1D Motion / Kinematics3h 56m
- Vectors, Scalars, & Displacement13m
- Average Velocity32m
- Intro to Acceleration7m
- Position-Time Graphs & Velocity26m
- Conceptual Problems with Position-Time Graphs22m
- Velocity-Time Graphs & Acceleration5m
- Calculating Displacement from Velocity-Time Graphs15m
- Conceptual Problems with Velocity-Time Graphs10m
- Calculating Change in Velocity from Acceleration-Time Graphs10m
- Graphing Position, Velocity, and Acceleration Graphs11m
- Kinematics Equations37m
- Vertical Motion and Free Fall19m
- Catch/Overtake Problems23m
- 3. Vectors2h 43m
- Review of Vectors vs. Scalars1m
- Introduction to Vectors7m
- Adding Vectors Graphically22m
- Vector Composition & Decomposition11m
- Adding Vectors by Components13m
- Trig Review24m
- Unit Vectors15m
- Introduction to Dot Product (Scalar Product)12m
- Calculating Dot Product Using Components12m
- Intro to Cross Product (Vector Product)23m
- Calculating Cross Product Using Components17m
- 4. 2D Kinematics1h 42m
- 5. Projectile Motion3h 6m
- 6. Intro to Forces (Dynamics)3h 22m
- 7. Friction, Inclines, Systems2h 44m
- 8. Centripetal Forces & Gravitation7h 26m
- Uniform Circular Motion7m
- Period and Frequency in Uniform Circular Motion20m
- Centripetal Forces15m
- Vertical Centripetal Forces10m
- Flat Curves9m
- Banked Curves10m
- Newton's Law of Gravity30m
- Gravitational Forces in 2D25m
- Acceleration Due to Gravity13m
- Satellite Motion: Intro5m
- Satellite Motion: Speed & Period35m
- Geosynchronous Orbits15m
- Overview of Kepler's Laws5m
- Kepler's First Law11m
- Kepler's Third Law16m
- Kepler's Third Law for Elliptical Orbits15m
- Gravitational Potential Energy21m
- Gravitational Potential Energy for Systems of Masses17m
- Escape Velocity21m
- Energy of Circular Orbits23m
- Energy of Elliptical Orbits36m
- Black Holes16m
- Gravitational Force Inside the Earth13m
- Mass Distribution with Calculus45m
- 9. Work & Energy1h 59m
- 10. Conservation of Energy2h 54m
- Intro to Energy Types3m
- Gravitational Potential Energy10m
- Intro to Conservation of Energy32m
- Energy with Non-Conservative Forces20m
- Springs & Elastic Potential Energy19m
- Solving Projectile Motion Using Energy13m
- Motion Along Curved Paths4m
- Rollercoaster Problems13m
- Pendulum Problems13m
- Energy in Connected Objects (Systems)24m
- Force & Potential Energy18m
- 11. Momentum & Impulse3h 40m
- Intro to Momentum11m
- Intro to Impulse14m
- Impulse with Variable Forces12m
- Intro to Conservation of Momentum17m
- Push-Away Problems19m
- Types of Collisions4m
- Completely Inelastic Collisions28m
- Adding Mass to a Moving System8m
- Collisions & Motion (Momentum & Energy)26m
- Ballistic Pendulum14m
- Collisions with Springs13m
- Elastic Collisions24m
- How to Identify the Type of Collision9m
- Intro to Center of Mass15m
- 12. Rotational Kinematics2h 59m
- 13. Rotational Inertia & Energy7h 4m
- More Conservation of Energy Problems54m
- Conservation of Energy in Rolling Motion45m
- Parallel Axis Theorem13m
- Intro to Moment of Inertia28m
- Moment of Inertia via Integration18m
- Moment of Inertia of Systems23m
- Moment of Inertia & Mass Distribution10m
- Intro to Rotational Kinetic Energy16m
- Energy of Rolling Motion18m
- Types of Motion & Energy24m
- Conservation of Energy with Rotation35m
- Torque with Kinematic Equations56m
- Rotational Dynamics with Two Motions50m
- Rotational Dynamics of Rolling Motion27m
- 14. Torque & Rotational Dynamics2h 5m
- 15. Rotational Equilibrium3h 39m
- 16. Angular Momentum3h 6m
- Opening/Closing Arms on Rotating Stool18m
- Conservation of Angular Momentum46m
- Angular Momentum & Newton's Second Law10m
- Intro to Angular Collisions15m
- Jumping Into/Out of Moving Disc23m
- Spinning on String of Variable Length20m
- Angular Collisions with Linear Motion8m
- Intro to Angular Momentum15m
- Angular Momentum of a Point Mass21m
- Angular Momentum of Objects in Linear Motion7m
- 17. Periodic Motion2h 9m
- 18. Waves & Sound3h 40m
- Intro to Waves11m
- Velocity of Transverse Waves21m
- Velocity of Longitudinal Waves11m
- Wave Functions31m
- Phase Constant14m
- Average Power of Waves on Strings10m
- Wave Intensity19m
- Sound Intensity13m
- Wave Interference8m
- Superposition of Wave Functions3m
- Standing Waves30m
- Standing Wave Functions14m
- Standing Sound Waves12m
- Beats8m
- The Doppler Effect7m
- 19. Fluid Mechanics4h 27m
- 20. Heat and Temperature3h 7m
- Temperature16m
- Linear Thermal Expansion14m
- Volume Thermal Expansion14m
- Moles and Avogadro's Number14m
- Specific Heat & Temperature Changes12m
- Latent Heat & Phase Changes16m
- Intro to Calorimetry21m
- Calorimetry with Temperature and Phase Changes15m
- Advanced Calorimetry: Equilibrium Temperature with Phase Changes9m
- Phase Diagrams, Triple Points and Critical Points6m
- Heat Transfer44m
- 21. Kinetic Theory of Ideal Gases1h 50m
- 22. The First Law of Thermodynamics1h 26m
- 23. The Second Law of Thermodynamics3h 11m
- 24. Electric Force & Field; Gauss' Law3h 42m
- 25. Electric Potential1h 51m
- 26. Capacitors & Dielectrics2h 2m
- 27. Resistors & DC Circuits3h 8m
- 28. Magnetic Fields and Forces2h 23m
- 29. Sources of Magnetic Field2h 30m
- Magnetic Field Produced by Moving Charges10m
- Magnetic Field Produced by Straight Currents27m
- Magnetic Force Between Parallel Currents12m
- Magnetic Force Between Two Moving Charges9m
- Magnetic Field Produced by Loops andSolenoids42m
- Toroidal Solenoids aka Toroids12m
- Biot-Savart Law (Calculus)18m
- Ampere's Law (Calculus)17m
- 30. Induction and Inductance3h 38m
- 31. Alternating Current2h 37m
- Alternating Voltages and Currents18m
- RMS Current and Voltage9m
- Phasors20m
- Resistors in AC Circuits9m
- Phasors for Resistors7m
- Capacitors in AC Circuits16m
- Phasors for Capacitors8m
- Inductors in AC Circuits13m
- Phasors for Inductors7m
- Impedance in AC Circuits18m
- Series LRC Circuits11m
- Resonance in Series LRC Circuits10m
- Power in AC Circuits5m
- 32. Electromagnetic Waves2h 14m
- 33. Geometric Optics2h 57m
- 34. Wave Optics1h 15m
- 35. Special Relativity2h 10m
10. Conservation of Energy
Gravitational Potential Energy
Struggling with Physics?
Join thousands of students who trust us to help them ace their exams!Watch the first video
Anderson Video - Gravitational Potential Energy
Professor Anderson
Video duration:
3mPlay a video:
Related Videos
Related Practice