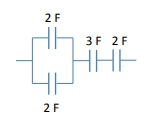
When working with circuits that involve capacitors, it's essential to understand how to simplify complex arrangements into a single equivalent capacitor. This process is crucial for analyzing circuits effectively. The concept of equivalent capacitance allows us to treat multiple capacitors as one, making calculations more manageable.
Capacitors can be connected in two primary configurations: series and parallel. In a series connection, capacitors are arranged one after the other, similar to watching a series of shows in a binge-watching session. The formula for calculating the equivalent capacitance (\(C_{EQ}\)) in a series configuration is given by the inverse sum of the individual capacitances:
\[\frac{1}{C_{EQ}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \ldots\]
It’s important to remember to take the reciprocal of the final sum to find \(C_{EQ}\). A common mistake is forgetting this step, which can lead to incorrect results.
In contrast, when capacitors are connected in parallel, they branch off into separate paths. The equivalent capacitance in this case is simply the sum of the individual capacitances:
\[C_{EQ} = C_1 + C_2 + C_3 + \ldots\]
This method is straightforward, as you just add the capacitances directly. Understanding these two configurations is fundamental for solving more complex circuits that may involve both series and parallel connections.
When faced with a circuit that has a combination of series and parallel capacitors, the approach is to simplify the circuit step by step, starting from the innermost arrangement. For example, if you have capacitors in parallel that are then in series with another capacitor, you would first calculate the equivalent capacitance of the parallel capacitors and then treat that result as a single capacitor in series with the other capacitor.
To illustrate, consider a circuit with two capacitors in parallel, each with capacitances of 2 Farads. The equivalent capacitance for this parallel arrangement would be:
\[C_{left} = 2 \, \text{F} + 2 \, \text{F} = 4 \, \text{F}\]
If this is in series with another capacitor of 5 Farads, the equivalent capacitance would be calculated as follows:
\[\frac{1}{C_{EQ}} = \frac{1}{C_{left}} + \frac{1}{C_{right}} = \frac{1}{4} + \frac{1}{5}\]
Finding a common denominator and summing gives:
\[\frac{1}{C_{EQ}} = \frac{5}{20} + \frac{4}{20} = \frac{9}{20}\]
Taking the reciprocal yields:
\[C_{EQ} = \frac{20}{9} \, \text{F}\]
This systematic approach of simplifying from the inside out is key to solving complex capacitor circuits. By mastering these principles, you can confidently tackle a variety of circuit problems involving capacitors.