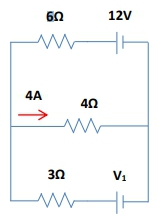
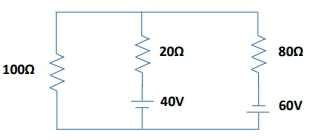
Kirchhoff's loop rule, also known as Kirchhoff's voltage law, is a fundamental principle in circuit analysis that states the sum of all voltages around a closed loop in a circuit must equal zero. This concept is crucial when dealing with complex circuits that contain multiple voltage sources, as it allows for systematic problem-solving. The essence of the loop rule is straightforward: as you traverse a loop, you will either add or subtract the voltages of the components based on their orientation relative to the direction of the current flow.
To apply Kirchhoff's loop rule effectively, one must first identify the direction of the current and the loop. The voltage across a resistor can be calculated using Ohm's law, expressed as \( V = I \cdot R \), where \( I \) is the current and \( R \) is the resistance. When writing a loop equation, it is essential to assign positive and negative signs to the voltages based on the direction of the current and the loop. If you cross a component from negative to positive, you add that voltage; conversely, if you cross from positive to negative, you subtract it.
For example, consider a loop with two resistors and two batteries. If you start at a point in the loop and move in the direction of the current, you would first encounter a resistor. The voltage across this resistor would be subtracted from the total because you are moving from positive to negative. If you then encounter a battery, the voltage would be added if you cross from negative to positive. This process continues until you return to the starting point, at which point the sum of all voltages should equal zero.
It is important to note that the direction in which you traverse the loop (clockwise or counterclockwise) does not affect the final equation; you will arrive at the same result regardless of the chosen direction. This flexibility allows for greater ease in circuit analysis, as you can select the direction that seems most intuitive for the problem at hand.
In summary, Kirchhoff's loop rule is a powerful tool for analyzing electrical circuits. By carefully considering the direction of current flow and the orientation of circuit elements, you can systematically write loop equations that facilitate the solution of complex circuit problems. Mastery of this rule will significantly enhance your ability to tackle a variety of circuit configurations.