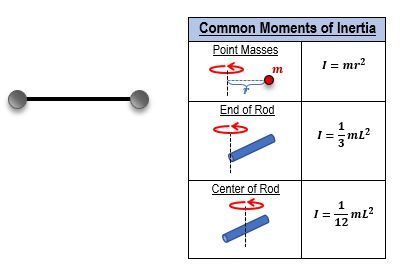
The moment of inertia is a fundamental concept in rotational dynamics, analogous to mass in linear motion. It quantifies an object's resistance to changes in its rotational velocity, much like mass measures resistance to changes in linear velocity. In linear motion, mass is a key factor in equations such as \( F = ma \) and kinetic energy \( KE = \frac{1}{2} mv^2 \). Similarly, the moment of inertia, denoted as \( I \), plays a crucial role in rotational motion equations.
In rotational dynamics, the moment of inertia depends on two primary factors: the mass of the object and its distance from the axis of rotation. This relationship can be visualized with a yo-yo; if it spins at different distances from the axis, its moment of inertia changes. The formula for the moment of inertia of a point mass is given by:
\[ I = mr^2 \]
where \( m \) is the mass and \( r \) is the distance from the axis of rotation. For rigid bodies, such as cylinders or spheres, the moment of inertia is determined using specific formulas found in reference tables, often expressed in the general form:
\[ I = k \cdot mr^2 \]
where \( k \) is a constant that varies depending on the shape of the object. For example, a solid cylinder rotating about its central axis has a moment of inertia of:
\[ I = \frac{1}{2} mR^2 \]
where \( R \) is the radius of the cylinder.
When calculating the moment of inertia for a system of objects, the total moment of inertia is the sum of the individual moments of inertia of each object. For instance, if a system consists of two point masses attached to a massless rod, the total moment of inertia can be calculated as:
\[ I_{\text{total}} = I_1 + I_2 + I_{\text{rod}} \]
In this scenario, if the rod is massless, its contribution to the moment of inertia is zero. Thus, the total moment of inertia would only include the contributions from the point masses, calculated using their respective distances from the axis of rotation.
The units of moment of inertia are expressed as kilogram meters squared (kg·m²), indicating the relationship between mass and the square of the distance from the axis of rotation. A higher moment of inertia signifies greater resistance to changes in rotational motion, making it more challenging to alter the object's angular velocity.
Understanding the moment of inertia is essential for analyzing rotational motion, as it directly influences how objects respond to applied torques and angular accelerations.