Understanding torques acting on disc-like objects, such as pulleys or cylinders, is crucial for solving more complex problems in physics. When a force is applied to a disc, the distance from the axis of rotation to the point where the force is applied, denoted as r, plays a significant role in determining the torque produced. It is important to note that this distance is not always the same as the radius of the disc.
For example, consider a system with two masses, m1 and m2, connected by a light string that wraps around a solid cylinder. The cylinder has a mass m3 and a radius R. When the blocks are released, the net torque on the cylinder can be calculated by summing the torques produced by the forces acting on it. The relevant forces include the gravitational forces acting on the masses and the weight of the cylinder itself.
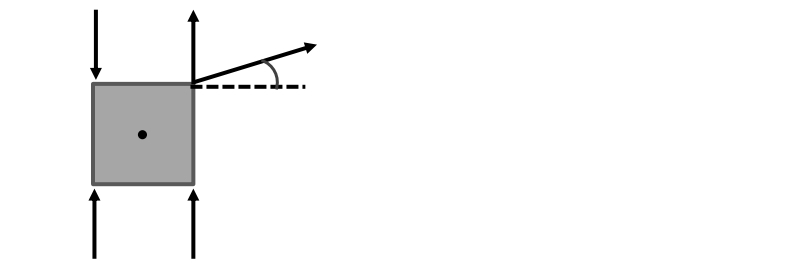
The torque produced by a force is calculated using the formula:
Torque = F × r × sin(θ)
where F is the force, r is the distance from the axis of rotation to the point of force application, and θ is the angle between the force vector and the r vector. In this scenario, the forces due to the weights of the cylinder and the tension do not produce any torque because they act directly at the axis of rotation, resulting in an r of zero or an angle of zero degrees, both of which yield a torque of zero.
The only forces that contribute to the net torque are those acting at the edges of the disc, specifically m1 and m2. For m1, the torque can be calculated as:
Torque1 = m1 × g × R × sin(90°) = m1 × g × R
For m2, the torque is similarly calculated:
Torque2 = -(m2 × g × R × sin(90°)) = -(m2 × g × R)
In this case, if m1 is 4 kg and m2 is 5 kg, with g approximated to 10 m/s² and R as 3 m, the calculations yield:
Torque1 = 4 kg × 10 m/s² × 3 m = 120 N·m (positive, counterclockwise)
Torque2 = - (5 kg × 10 m/s² × 3 m) = -150 N·m (negative, clockwise)
Summing these torques gives the net torque:
Net Torque = 120 N·m - 150 N·m = -30 N·m
This negative value indicates that the net torque is in the clockwise direction. Understanding these principles of torque is essential for analyzing rotational motion and the dynamics of systems involving disc-like objects.