Bonferroni Test Shown below are weights (kg) of poplar trees obtained from trees planted in a rich and moist region. The trees were given different treatments identified in the table below. The data are from a study conducted by researchers at Pennsylvania State University and were provided by Minitab, Inc. Also shown are partial results from using the Bonferroni test with the sample data.

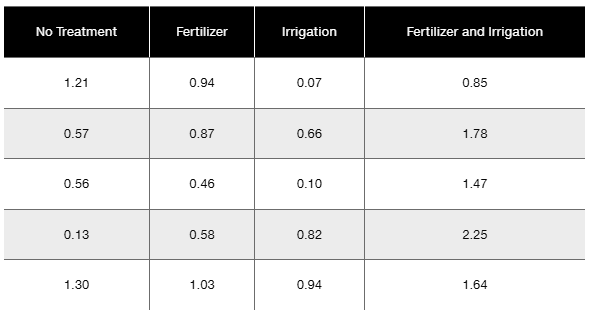
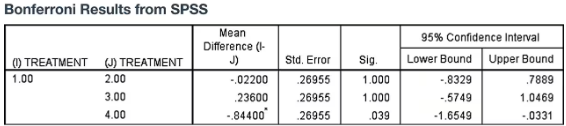
b. What do the displayed Bonferroni SPSS results tell us?

Verified step by step guidance

1. Step 1: Understand the context of the Bonferroni test. It is a post-hoc multiple comparison test used after an ANOVA to determine which specific group means are significantly different from each other while controlling the overall Type I error rate.
2. Step 2: Identify the treatments being compared. The treatments are No Treatment (1), Fertilizer (2), Irrigation (3), and Fertilizer and Irrigation (4). The Bonferroni results table compares the mean differences between No Treatment (1) and each of the other treatments.
3. Step 3: Interpret the 'Mean Difference (I-J)' column. This shows the difference in average weights between the No Treatment group and each other treatment group. For example, the difference between No Treatment and Fertilizer is -0.02200, indicating the Fertilizer group has a slightly lower mean weight than No Treatment.
4. Step 4: Look at the 'Sig.' (significance) column to determine if the differences are statistically significant. A value less than the chosen alpha level (commonly 0.05) indicates a significant difference. Here, the significance values for comparisons with Fertilizer and Irrigation are 1.000 and 0.393 respectively, which are not significant, but the comparison with Fertilizer and Irrigation combined is 0.039, which is significant.
5. Step 5: Examine the 95% confidence intervals for the mean differences. If the interval includes zero, it suggests no significant difference. For the Fertilizer and Irrigation combined treatment, the confidence interval does not include zero (-1.6549 to -0.0331), confirming the significant difference found in the significance column.

Key Concepts

Bonferroni Test

The Bonferroni test is a multiple comparison procedure used after an ANOVA to control the overall Type I error rate when making pairwise comparisons. It adjusts the significance level by dividing it by the number of comparisons, making it more stringent to declare differences significant. This helps prevent false positives when testing multiple hypotheses simultaneously.

Interpretation of SPSS Bonferroni Output

The SPSS Bonferroni output shows pairwise mean differences between treatment groups, their standard errors, significance values (p-values), and confidence intervals. A significant p-value (typically < 0.05) indicates a statistically significant difference between the two treatment means. Confidence intervals that do not include zero also support significant differences.

Multiple Comparisons in Experimental Design

In experiments with multiple treatment groups, multiple comparisons are necessary to identify which groups differ. However, conducting many tests increases the chance of Type I errors. Methods like the Bonferroni correction adjust for this by controlling the family-wise error rate, ensuring that the overall probability of making one or more false discoveries remains low.