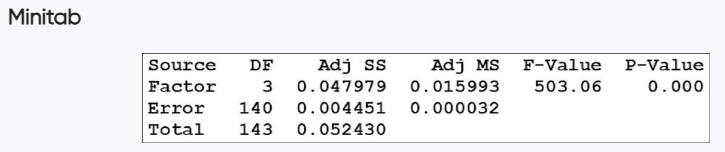
Cola Weights Data Set 37 “Cola Weights and Volumes” in Appendix B lists the weights (lb) of the contents of cans of cola from four different samples: (1) regular Coke, (2) Diet Coke, (3) regular Pepsi, and (4) Diet Pepsi. The results from analysis of variance are shown in the Minitab display below. What is the null hypothesis for this analysis of variance test? Based on the displayed results, what should you conclude about H_knot. What do you conclude about equality of the mean weights from the four samples?

Verified step by step guidance

1. Step 1: Understand the null hypothesis (H₀) for an analysis of variance (ANOVA) test. The null hypothesis states that the mean weights of the contents of the cans from the four samples (regular Coke, Diet Coke, regular Pepsi, Diet Pepsi) are equal. Mathematically, H₀: μ₁ = μ₂ = μ₃ = μ₄, where μ represents the mean weight for each sample.
2. Step 2: Examine the Minitab output provided. Focus on the P-Value column, which is used to test the null hypothesis. The P-Value for the 'Factor' source is 0.000, which is significantly less than the common significance level of 0.05.
3. Step 3: Interpret the P-Value. Since the P-Value is less than 0.05, we reject the null hypothesis (H₀). This indicates that there is sufficient evidence to conclude that at least one of the mean weights is different from the others.
4. Step 4: Analyze the F-Value. The F-Value is 503.06, which is very large. A high F-Value further supports the conclusion that the variation between the group means is significant compared to the variation within the groups.
5. Step 5: Conclude about the equality of mean weights. Based on the results, we conclude that the mean weights of the contents of the cans from the four samples are not equal. There is a statistically significant difference in the mean weights among the four groups.

Key Concepts

Null Hypothesis (H0)

The null hypothesis (H0) is a statement that there is no effect or no difference, and it serves as a starting point for statistical testing. In the context of the ANOVA test for the cola weights, H0 posits that the mean weights of the four cola samples (regular Coke, Diet Coke, regular Pepsi, and Diet Pepsi) are equal. Rejecting H0 suggests that at least one sample mean is different from the others.

Analysis of Variance (ANOVA)

ANOVA is a statistical method used to compare the means of three or more groups to determine if at least one group mean is significantly different from the others. It assesses the variance within each group and between groups, providing an F-value that indicates the ratio of these variances. A significant F-value, as shown in the Minitab output, suggests that the group means are not all equal.

P-Value

The P-value is a statistical measure that helps determine the significance of the results obtained from a hypothesis test. It represents the probability of observing the data, or something more extreme, assuming the null hypothesis is true. In the provided Minitab output, a P-value of 0.000 indicates strong evidence against the null hypothesis, leading to the conclusion that there are significant differences in the mean weights of the cola samples.