[NOW WORK] Job Satisfaction Is there an association between one’s level of education and satisfaction with work? A random sample of 5244 employed individuals were asked to disclose their highest level of education and satisfaction with their work/job. The results are shown in the table below. The data are from the General Social Survey.

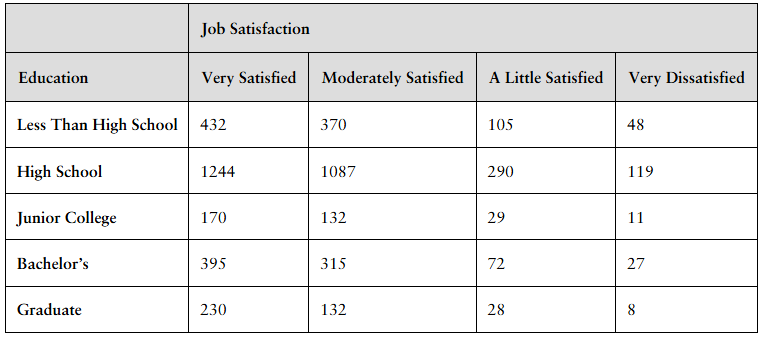
b. Verify that the requirements for performing a chi-square test of independence are satisfied.

Verified step by step guidance

1. Step 1: Identify the type of test and data structure. Since we want to check if there is an association between two categorical variables (Education level and Job Satisfaction), a chi-square test of independence is appropriate. The data is presented in a contingency table with counts for each combination of education level and job satisfaction category.
2. Step 2: Check the assumptions for the chi-square test of independence. The main requirements are: (a) The data should be from a random sample, (b) The observations should be independent, and (c) The expected frequency in each cell of the contingency table should be at least 5.
3. Step 3: Verify randomness and independence. The problem states that the sample is random, and since individuals are independently surveyed, the independence assumption is satisfied.
4. Step 4: Calculate the expected counts for each cell using the formula: \[\text{Expected Count} = \frac{(\text{Row Total}) \times (\text{Column Total})}{\text{Grand Total}}\]. This step is necessary to check if all expected counts are at least 5.
5. Step 5: Confirm that all expected counts are 5 or greater. If any expected count is less than 5, the chi-square test may not be valid, and an alternative method or combining categories might be needed. If all expected counts meet this criterion, the requirements for the chi-square test of independence are satisfied.

Key Concepts

Chi-Square Test of Independence

This test determines whether there is a significant association between two categorical variables. It compares observed frequencies in each category to expected frequencies under the assumption of independence. A large difference suggests a relationship between variables.

Requirements for Chi-Square Test

Key conditions include: data must be from a random sample, categories must be mutually exclusive, and expected cell counts should generally be at least 5 to ensure validity. These requirements ensure the test's assumptions are met for accurate results.

Contingency Table Analysis

A contingency table displays the frequency distribution of variables and helps visualize the relationship between them. It is essential for calculating observed and expected counts, which are used in the chi-square test to assess independence.