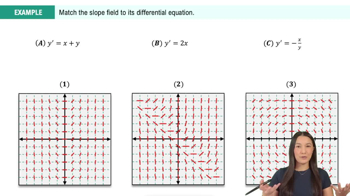
13. Intro to Differential Equations

Sketch a slope field for the following differential equation through the nine points shown on the graph. 

$y^{\prime }=y-xy$

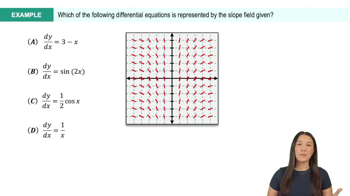
Shown above is a slope field for which of the following differential equations?

Which of the following differential equations could produce a slope field where the slope at each point $(x,y)$ is given by $y^3-x$?

17–20. Increasing and decreasing solutions Consider the following differential equations. A detailed direction field is not needed.

b. In what regions are solutions increasing? Decreasing?

y'(t) = (y−1)(1+y)

17–20. Increasing and decreasing solutions Consider the following differential equations. A detailed direction field is not needed.

a. Find the solutions that are constant, for all t ≥ 0 (the equilibrium solutions).

y'(t) = (y−2)(y+1)

17–20. Increasing and decreasing solutions Consider the following differential equations. A detailed direction field is not needed.

c. Which initial conditions y(0) = A lead to solutions that are increasing in time? Decreasing?

y'(t) = cos y for |y| ≤ π

17–20. Increasing and decreasing solutions Consider the following differential equations. A detailed direction field is not needed.

b. In what regions are solutions increasing? Decreasing?

y'(t) = y(y+3)(4-y)