In rotational dynamics, understanding the relationship between torque, moment of inertia, and angular acceleration is crucial. The fundamental equation governing this relationship is given by:
Torque (τ) = I * α
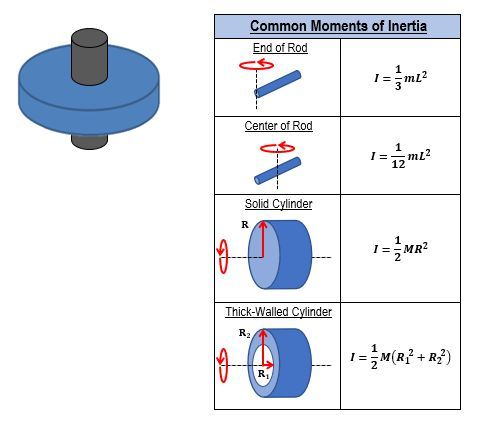
Here, τ represents torque, I is the moment of inertia, and α is the angular acceleration. The moment of inertia for a solid sphere is defined as:
I = \frac{2}{5} m r^2
where m is the mass and r is the radius of the sphere. When dealing with rotational motion, it is essential to convert any given rotational speed in revolutions per minute (RPM) to angular velocity (ω) in radians per second. This conversion is done using the formula:
ω = 2πf
where f is the frequency in revolutions per second, calculated as:
f = \frac{RPM}{60}
For example, if a solid sphere has a mass of 200 kg and a diameter of 6 meters (which gives a radius of 3 meters), and it is spinning at 180 RPM clockwise, we first convert this to angular velocity:
ω = 2π \left(-\frac{180}{60}\right) = -6π \text{ radians/second}
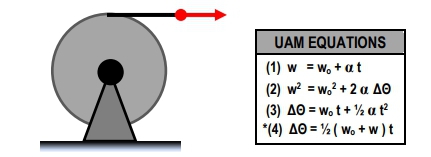
To find the torque required to stop the sphere in a specified time, we need to determine the angular acceleration (α). The relationship between the initial and final angular velocities and angular acceleration is given by the equation:
ω_f = ω_i + αt
Rearranging this to solve for α gives:
α = \frac{ω_f - ω_i}{t}
In this scenario, if we want to stop the sphere (ω_f = 0) in 10 seconds (t = 10), we can substitute the values:
α = \frac{0 - (-6π)}{10} = \frac{6π}{10} = 1.88 \text{ radians/second}^2
Now that we have α, we can substitute it back into the torque equation. First, we calculate the moment of inertia:
I = \frac{2}{5} (200) (3^2) = \frac{2}{5} (200) (9) = 720 \text{ kg m}^2
Finally, substituting I and α into the torque equation gives:
τ = I * α = 720 * 1.88 = 1353.6 \text{ Newton meter}
This example illustrates the interconnectedness of torque, angular acceleration, and moment of inertia in solving rotational motion problems. By systematically applying the relevant equations and converting units as necessary, one can effectively analyze and solve complex rotational dynamics scenarios.