Electric flux is a fundamental concept in electrostatics, crucial for understanding and applying Gauss's law. It quantifies how much of an electric field passes through a given surface, similar to measuring the flow of water through a ring placed in a river. The electric flux (\(\Phi_E\)) can be visualized as the number of electric field lines that intersect a surface area.
To define electric flux mathematically, we use the equation:
\[\Phi_E = E \cdot A \cdot \cos(\theta)\]
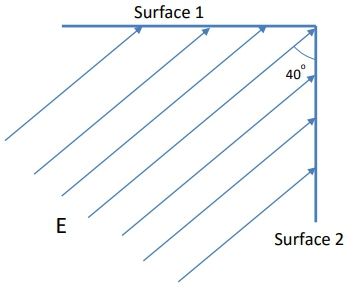
Here, \(E\) represents the magnitude of the electric field, \(A\) is the area of the surface, and \(\theta\) is the angle between the electric field lines and the normal (perpendicular) vector to the surface. The normal vector is crucial as it helps determine how effectively the electric field penetrates the surface.
Electric flux can vary based on the orientation of the surface relative to the electric field. If the surface is aligned with the field (i.e., \(\theta = 0^\circ\)), the flux is maximized. Conversely, if the surface is perpendicular to the field (i.e., \(\theta = 90^\circ\)), no electric field lines pass through, resulting in zero flux. When the surface is at an angle, the flux is a partial amount, depending on the cosine of the angle.
When considering a closed surface, such as a cube, the total electric flux through the surface is the sum of the electric fluxes through each individual face. This is expressed as:
\[\Phi_{\text{net}} = \Phi_1 + \Phi_2 + \Phi_3 + \Phi_4 + \Phi_5 + \Phi_6\]
In this context, positive flux indicates that electric field lines are exiting the surface, while negative flux indicates that they are entering. The directionality of the electric field relative to the normal vector determines the sign of the flux. For example, if the electric field and the normal vector point in the same direction, the flux is positive; if they point in opposite directions, the flux is negative.
To illustrate, if you calculate the total flux through a cube with individual flux values of \(100\), \(20\), \(-40\), and \(-80\), the net flux would be:
\[\Phi_{\text{net}} = 100 + 20 - 40 - 80 = 0\]
This example demonstrates how to sum the contributions of each face to find the overall electric flux through a closed surface. Understanding electric flux is essential for solving problems in electrostatics and applying Gauss's law effectively.