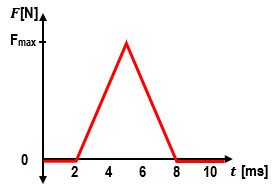
In physics, impulse is a crucial concept that relates to the change in momentum of an object. When analyzing force versus time graphs, the impulse can be determined by calculating the area under the curve of the graph. This is analogous to how work is calculated from force versus position graphs, where the area under the curve represents the work done. In the case of force versus time graphs, areas above the time axis correspond to positive impulse, while areas below indicate negative impulse.
To calculate impulse from a force versus time graph, one can break the graph into distinct geometric shapes, such as triangles and rectangles, and compute the area of each shape. For example, if a graph shows a force that varies over time, the impulse can be found by summing the areas of these shapes. The formula for the area of a triangle is given by:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
And for a rectangle, it is simply:
\[ \text{Area} = \text{base} \times \text{height} \]
Once the areas are calculated, they can be added together to find the total impulse. For instance, if the total area above the time axis is 30 Newton-seconds and the total area below is -17.5 Newton-seconds, the overall impulse would be:
\[ \text{Impulse} = 30 + (-17.5) = 12.5 \text{ Newton-seconds} \]
This positive impulse indicates that the net effect of the forces applied over the time interval resulted in a forward momentum change.
Furthermore, impulse is directly related to momentum through the equation:
\[ J = \Delta p = m \cdot v_{\text{final}} - m \cdot v_{\text{initial}} \]
Where \( J \) is the impulse, \( m \) is the mass, and \( v \) represents velocity. If an object starts from rest, the initial velocity is zero, simplifying the equation to:
\[ J = m \cdot v_{\text{final}} \]
In a practical example, if a remote-controlled car has a mass of 2 kilograms and the calculated impulse is 12.5 Newton-seconds, the final velocity can be determined by rearranging the equation:
\[ v_{\text{final}} = \frac{J}{m} = \frac{12.5}{2} = 6.25 \text{ meters per second} \]
This calculation illustrates how impulse not only quantifies the effect of forces over time but also provides insight into the resulting motion of an object.