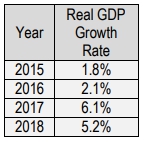
Understanding growth rates is crucial for analyzing economic performance, particularly in relation to Gross Domestic Product (GDP). The annual growth rate is calculated using a simple percentage change formula: the current GDP minus the previous year's GDP, divided by the previous year's GDP. This can be expressed mathematically as:
Annual Growth Rate = \(\frac{\text{Current GDP} - \text{Previous GDP}}{\text{Previous GDP}} \times 100\)
To find the average annual growth rate over multiple years, one can sum the growth rates for each year and divide by the number of years. This is akin to calculating an average score in a class, where you add up all the grades and divide by the total number of exams taken. The formula for average annual growth rate is:
Average Annual Growth Rate = \(\frac{\text{Sum of Growth Rates}}{\text{Number of Years}}\)
Another important concept is the Rule of 70, which estimates the time required for a value to double based on its growth rate. This rule states that the number of years it takes for a quantity to double is approximately equal to 70 divided by the growth rate. The formula is:
Years to Double = \(\frac{70}{\text{Growth Rate}}\)
When applying the Rule of 70, it is essential to input the growth rate as a whole number rather than a decimal. For example, a growth rate of 2% should be entered as 2, not 0.02. This approximation can yield significant insights into economic growth. For instance, if the growth rates are 2%, 4%, and 6%, the time to double would be approximately 35 years, 17.5 years, and 11.67 years, respectively. This illustrates how even small differences in growth rates can lead to substantial variations in the time it takes for an economy to double, ultimately impacting the standard of living.
In summary, analyzing growth rates through these calculations not only provides a clearer picture of economic health but also emphasizes the importance of sustained growth for improving living standards over time.