Effects of Taxes on a Market: Videos & Practice Problems

When a per unit tax is imposed, tax revenue equals the tax amount multiplied by the reduced quantity exchanged, represented as $T\cdot \mathrm{Q_T}$. This tax creates a wedge between buyer and seller prices, reducing consumer and producer surplus and generating tax revenue. The loss in total economic surplus, including consumer and producer surplus plus tax revenue, results in deadweight loss, shown by the untraded quantity areas. Understanding these market distortions highlights how taxes affect equilibrium, economic efficiency, and the balance between government revenue and market welfare.

Tax Revenue

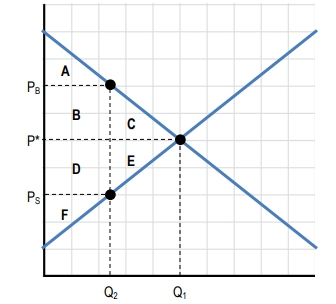
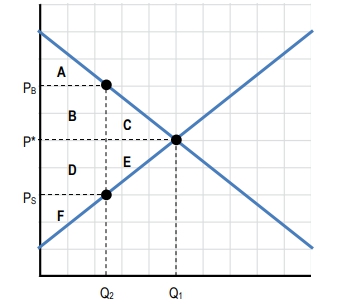
Understanding the impact of taxes on a market involves analyzing shifts in supply or demand curves and calculating the resulting tax revenue. When a per unit tax is imposed, it typically shifts either the supply or demand curve. For example, a tax on sellers shifts the supply curve to the left, reducing the quantity sold in the market. The new equilibrium quantity after the tax, denoted as \(q_t\), is found where the shifted supply curve intersects the original demand curve.

At this new equilibrium, the price buyers pay (\(P_b\)) is higher than the price sellers receive (\(P_s\)) due to the tax. The difference between these two prices represents the per unit tax rate, calculated as:

\[\text{Tax per unit} = P_b - P_s\]

The total tax revenue collected by the government is the product of this per unit tax and the quantity sold after the tax is imposed. This can be expressed as:

\[\text{Tax Revenue} = (P_b - P_s) \times q_t\]

Graphically, tax revenue is illustrated as the area of a rectangle on the supply and demand diagram. The height of this rectangle corresponds to the per unit tax (the vertical distance between \(P_b\) and \(P_s\)), and the width corresponds to the quantity sold after tax (\(q_t\)). This visual representation helps in understanding how taxes reduce the quantity traded and generate revenue.

For instance, if buyers pay \$10 per unit and sellers receive \$7 per unit after a tax, the per unit tax is \$3. If the quantity sold after tax is 10 units, then the total tax revenue is:

\[3 \times 10 = 30\]

Recognizing how to calculate and illustrate tax revenue on supply and demand diagrams is essential for analyzing the economic effects of taxation. This approach not only quantifies government revenue but also highlights the changes in market equilibrium caused by taxes, providing a foundation for deeper exploration of tax incidence and efficiency in markets.

Effects of Taxes

When a tax is imposed on a market, it generates tax revenue for the government, which can be calculated using the formula:

Tax Revenue = Tax Amount × Quantity Sold (QT)

This tax revenue is represented graphically as a rectangle, where the height is the tax amount and the width is the quantity exchanged after the tax is applied. The introduction of a tax disrupts market equilibrium, leading to different prices for buyers and sellers, which in turn affects economic surplus.

Economic surplus is the sum of consumer surplus and producer surplus. In a tax-free market, at equilibrium price (P*), consumer surplus includes the area above the price and below the demand curve, while producer surplus is the area below the price and above the supply curve. Together, they maximize total surplus, represented by the areas A, B, C (consumer surplus) and D, E, F (producer surplus).

However, when a tax is introduced, consumer surplus decreases significantly. The new consumer surplus is only the area above the buyer's price and below the demand curve, which is now just area A. Producer surplus also diminishes, as producers receive a lower price, resulting in only area F being counted as surplus. The areas B and D represent the tax revenue generated, which is the rectangle formed by the tax amount and the quantity sold after the tax.

Despite the tax revenue being a part of the total economic surplus, the overall surplus decreases due to the loss of areas C and E, which are no longer part of consumer and producer surplus. This loss is termed deadweight loss, represented by the areas C and E, indicating trades that do not occur because the market is no longer operating at the efficient quantity.

In summary, while a tax generates revenue for the government, it also leads to a reduction in economic surplus and creates deadweight loss, illustrating the trade-offs involved in tax policy. The overall economic surplus after a tax is calculated as:

Total Economic Surplus = Consumer Surplus (A) + Producer Surplus (F) + Tax Revenue (B + D)

However, it is important to note that the total surplus is less than it would be without the tax, highlighting the inefficiencies introduced by taxation in the market.

If a tax has caused the market-clearing quantity to fall to Q₂, what is consumer surplus?

• A. The area of (A)
• B. The area of (A), (B), and (C)
• C. The area of (A), (B), (C), (D), and (E)
• D. The area of (A), (B), (C), (D), (E), and (F)
• E. The area of (C) and (E)

Answer: (A)

If a tax has caused the market-clearing quantity to fall to Q₂, what is total economic surplus?

• A. The area of (A) and (F)
• B. The area of (D), (E), and (F)
• C. The area of (A), (B), (D), and (F)
• D. The area of (A), (B), (C), (D), (E), and (F)
• E. The area of (C) and (E)

Answer: (C)

Here’s what students ask on this topic:

What is the effect of a per unit tax on market equilibrium?

When a per unit tax is imposed on a market, it creates a wedge between the price buyers pay and the price sellers receive. This tax shifts the market away from its original equilibrium, reducing the quantity exchanged. The new quantity traded is lower than the equilibrium quantity, causing some mutually beneficial trades not to occur. As a result, the market is no longer efficient, and economic surplus decreases. The tax revenue collected by the government equals the per unit tax multiplied by the quantity exchanged under the tax. This situation leads to a loss in total surplus, known as deadweight loss, which represents the value of trades that no longer happen due to the tax.

How do taxes affect consumer surplus and producer surplus in a market?

Taxes reduce both consumer surplus and producer surplus. Consumer surplus is the area above the price paid by consumers and below the demand curve. When a tax is imposed, consumers pay a higher price, so their surplus shrinks, losing areas labeled B and C on the graph. Producer surplus is the area below the price received by producers and above the supply curve. With a tax, producers receive a lower price, reducing their surplus by areas D and E. The lost surplus from consumers and producers partly transfers to the government as tax revenue, but some surplus is lost entirely, creating deadweight loss.

What is deadweight loss and how is it related to taxes?

Deadweight loss is the loss of economic efficiency that occurs when the quantity of a good traded is below the market equilibrium due to a tax. It represents the value of trades that no longer happen because the tax increases the price buyers pay and decreases the price sellers receive. Graphically, deadweight loss is shown as the areas C and E, which are the surplus lost from consumers and producers that is not recovered as tax revenue. This loss means the market is not allocating resources efficiently, and total economic surplus is reduced.

How is tax revenue calculated in a market with a per unit tax?

Tax revenue in a market with a per unit tax is calculated by multiplying the tax amount per unit by the quantity of goods exchanged after the tax is imposed. Mathematically, this is expressed as $\mathrm{Tax\; Revenue}=\mathrm{Tax\; per\; unit}\cdot \mathrm{Quantity\; with\; tax}$. Graphically, this revenue is represented by a rectangle where the height is the tax per unit and the width is the quantity traded under the tax. This revenue is a transfer from consumers and producers to the government.

Why does imposing a tax lead to a loss in total economic surplus?

Imposing a tax reduces total economic surplus because it decreases the quantity traded below the efficient market equilibrium. While some surplus is transferred to the government as tax revenue, the tax also causes a reduction in consumer and producer surplus that is not offset by tax revenue. This lost surplus is called deadweight loss and represents the value of trades that no longer occur due to the tax. Therefore, the total economic surplus, which includes consumer surplus, producer surplus, and tax revenue, is less than it would be without the tax, indicating inefficiency in the market.