Understanding the concept of elasticity along a linear demand curve is crucial for analyzing how price changes affect quantity demanded. While slope and elasticity are related, they are fundamentally different. The slope measures the ratio of changes between two variables in specific units, whereas elasticity measures the ratio of percentage changes, highlighting the significance of percentage calculations in economic analysis.
For instance, consider a price increase from \$1 to \$2. The unit change is \$1, but the percentage change is 100%, as the price doubled. Conversely, increasing the price from \$2 to \$3 results in a unit change of \$1, but only a 50% increase, illustrating how larger initial values lead to smaller percentage changes. This distinction is vital when evaluating demand elasticity along a linear demand curve.
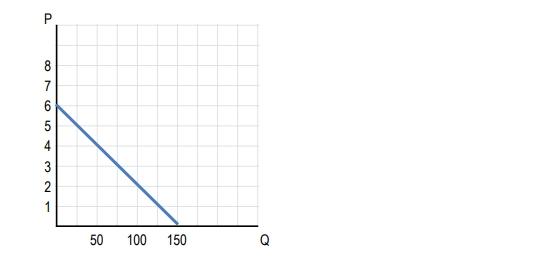
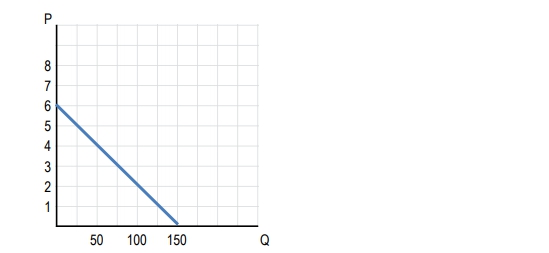
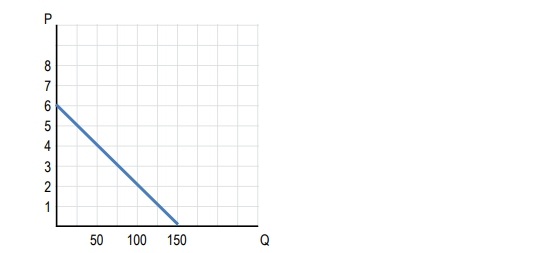
A linear demand curve consists of sections that exhibit different elasticities. To the left of the midpoint, demand is elastic, meaning that percentage changes in quantity demanded are greater than percentage changes in price. To the right of the midpoint, demand is inelastic, where percentage changes in price exceed those in quantity demanded. The midpoint itself represents unit elasticity, where total revenue is maximized.
Total revenue (TR) is calculated as the product of price (P) and quantity demanded (Q):
TR = P × Q
As price decreases and quantity demanded increases, total revenue initially rises until it reaches a peak at the unit elastic point. Beyond this point, further price decreases lead to a decline in total revenue, as the increase in quantity demanded does not compensate for the loss in price. This behavior can be visualized in a graph where total revenue is plotted against quantity, showing an increase to a maximum point before declining.
In summary, when analyzing a linear demand curve, remember that demand is elastic to the left of the midpoint, unit elastic at the midpoint, and inelastic to the right. This understanding is essential for making informed pricing and production decisions that maximize revenue.